数据挖掘梳理
目录:
- 数据挖掘的应用
- 电商平台:价格预测、销量预测、推荐系统、库存预测、广告智能投放、智能客服、欺诈检测
- 游戏平台:游戏AI角色、玩家行为预测、购买道具预测
- 信用卡:mgm拉新预测、逾期预测、分期用户预测、客户流失预测
- 建模的步骤
- 数据获取
- 外部数据
- 爬虫采集
- 购买
- 内部数据
- hive、mysql、Oracle、mango、Redis,sqlite、Elasticsearch
- 外部数据
- 数据预处理
- 缺失值处理
- 特征变换
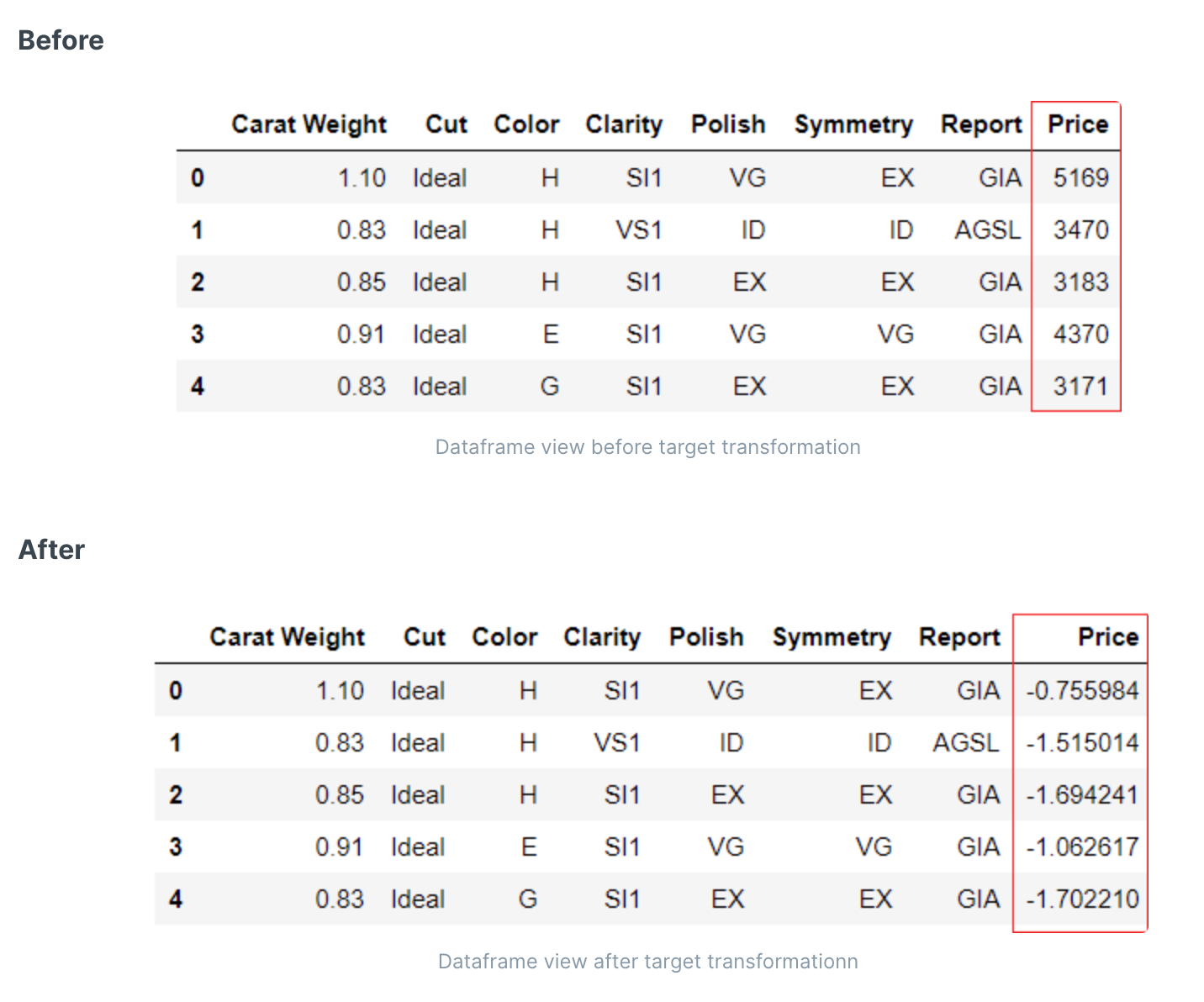
- 目标转换(回归)
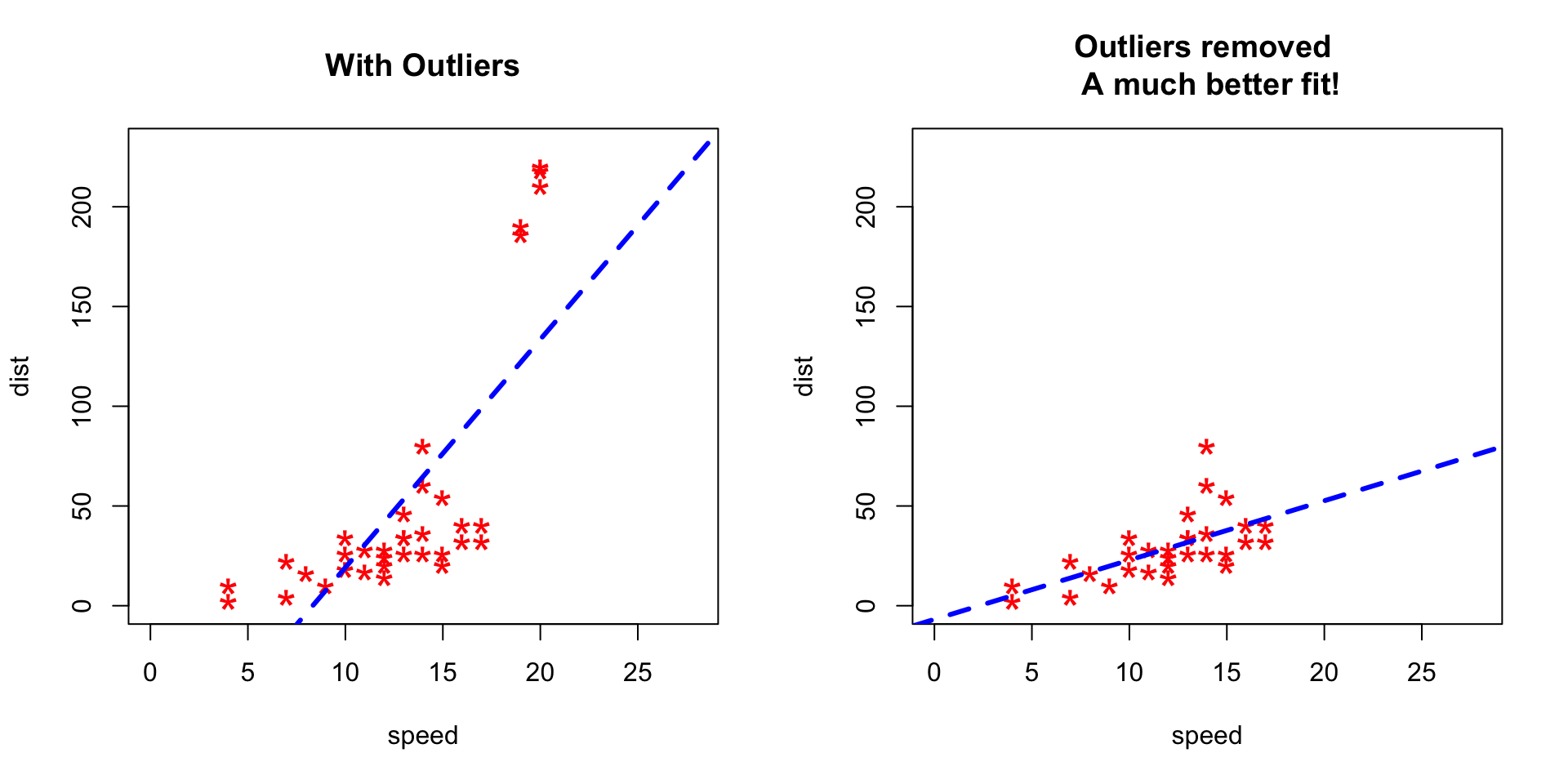
- 异常值识别及删除
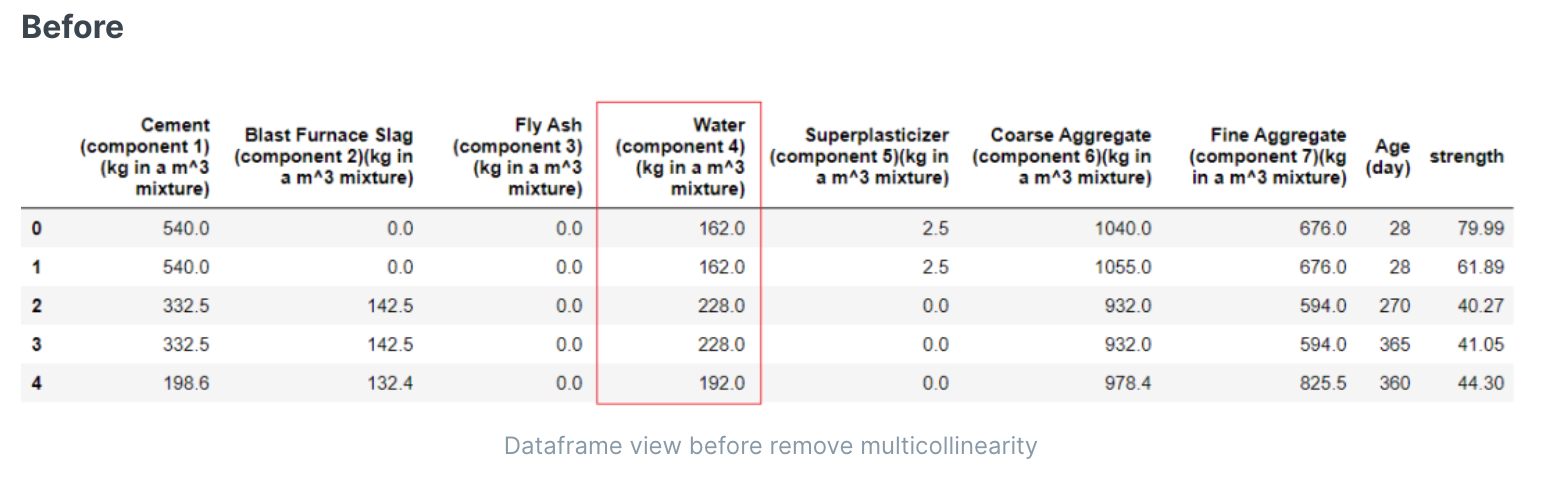
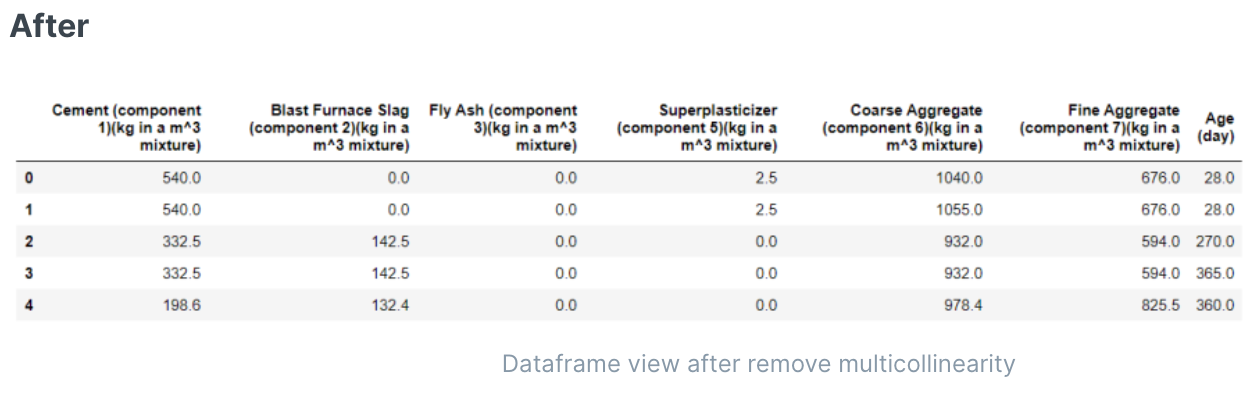
- 删除相关性太高的特征
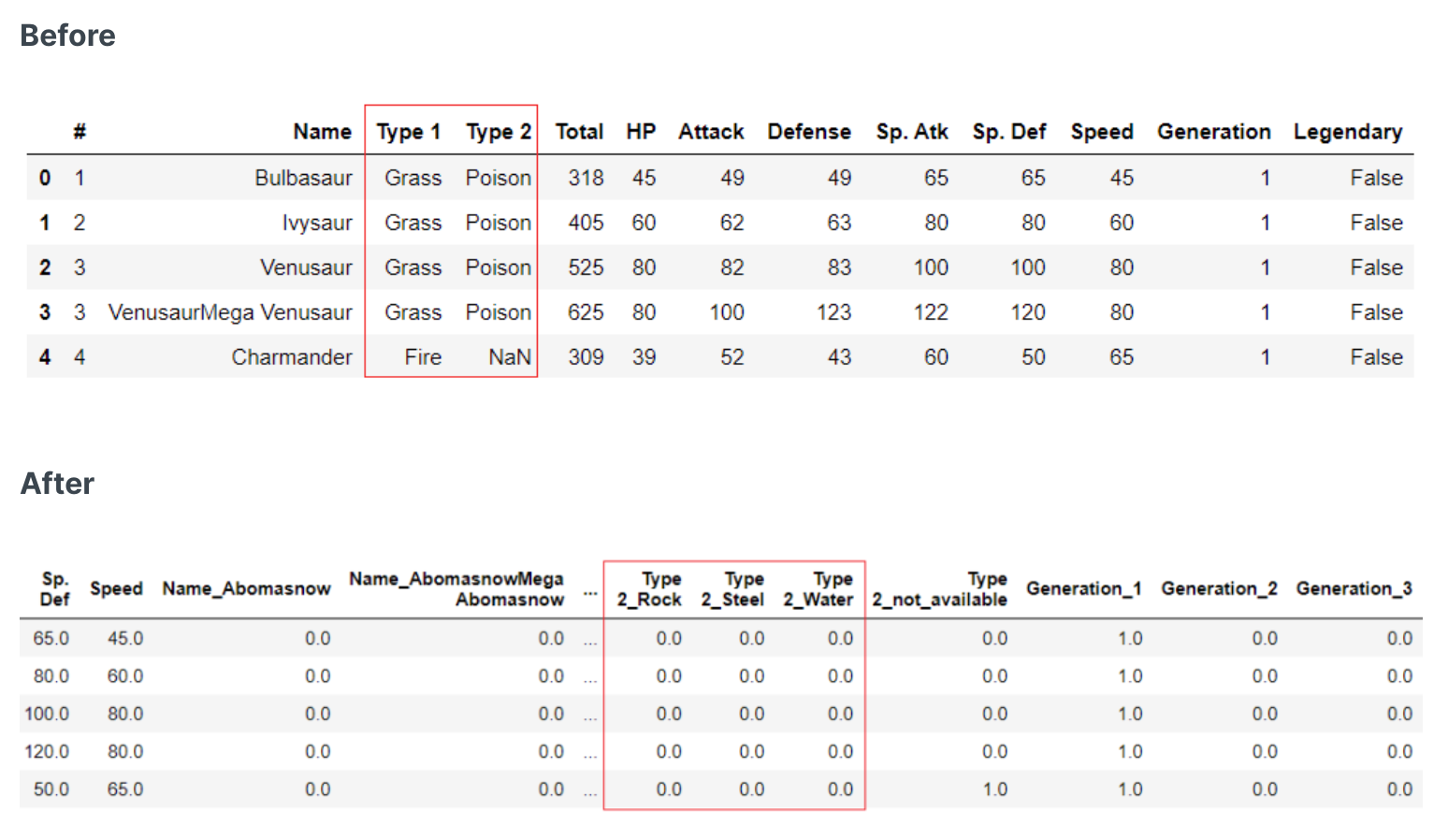
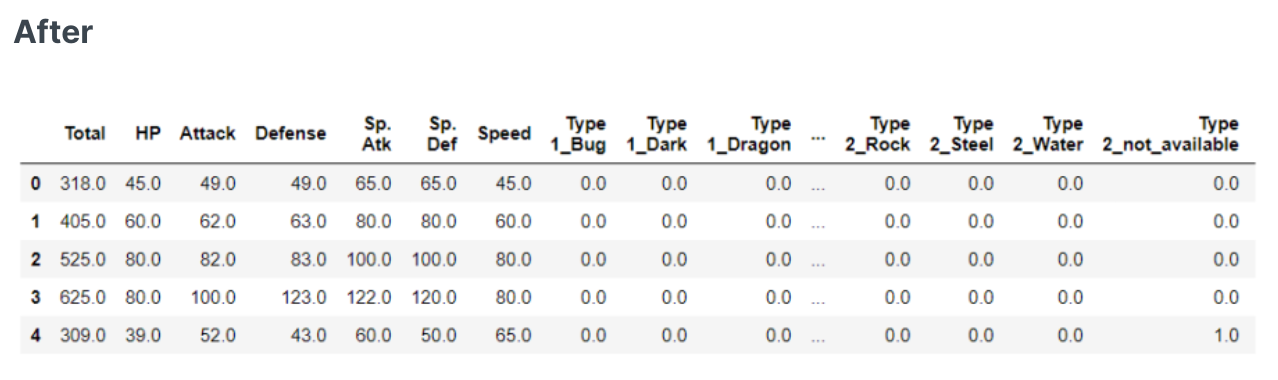
- 特征one-hot热编码
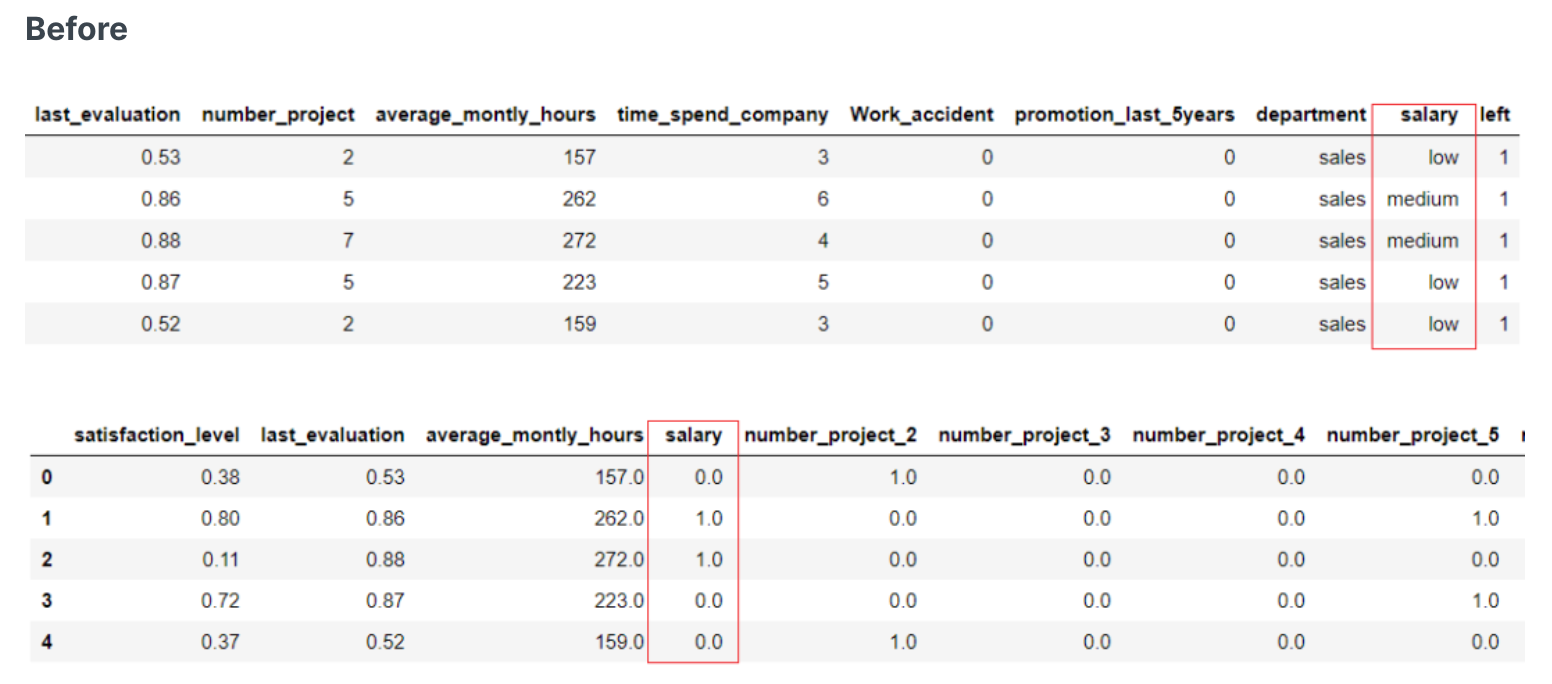
- 特征顺序编码
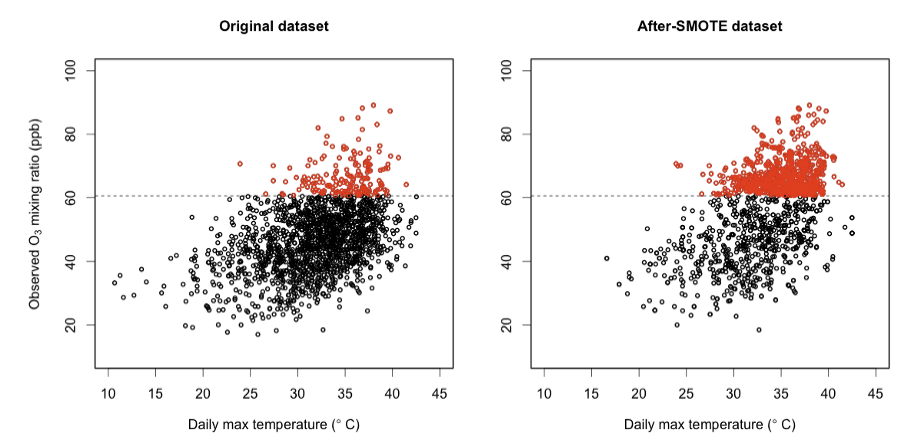
- 目标类别不均衡处理(分类)
- 特征工程
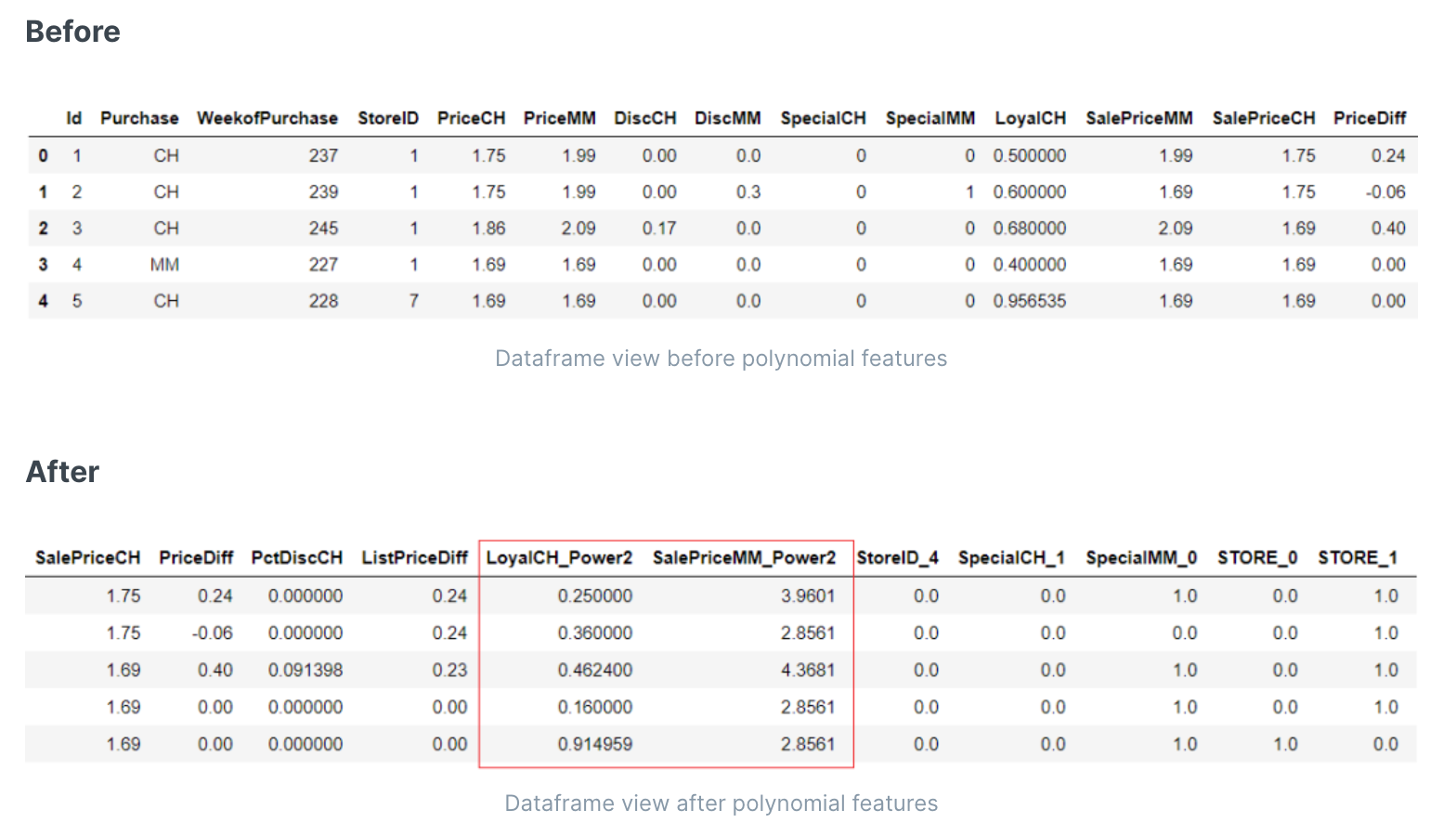
- 生成多项式特征(如a,b特征,生成特征c=a^2+b^2)
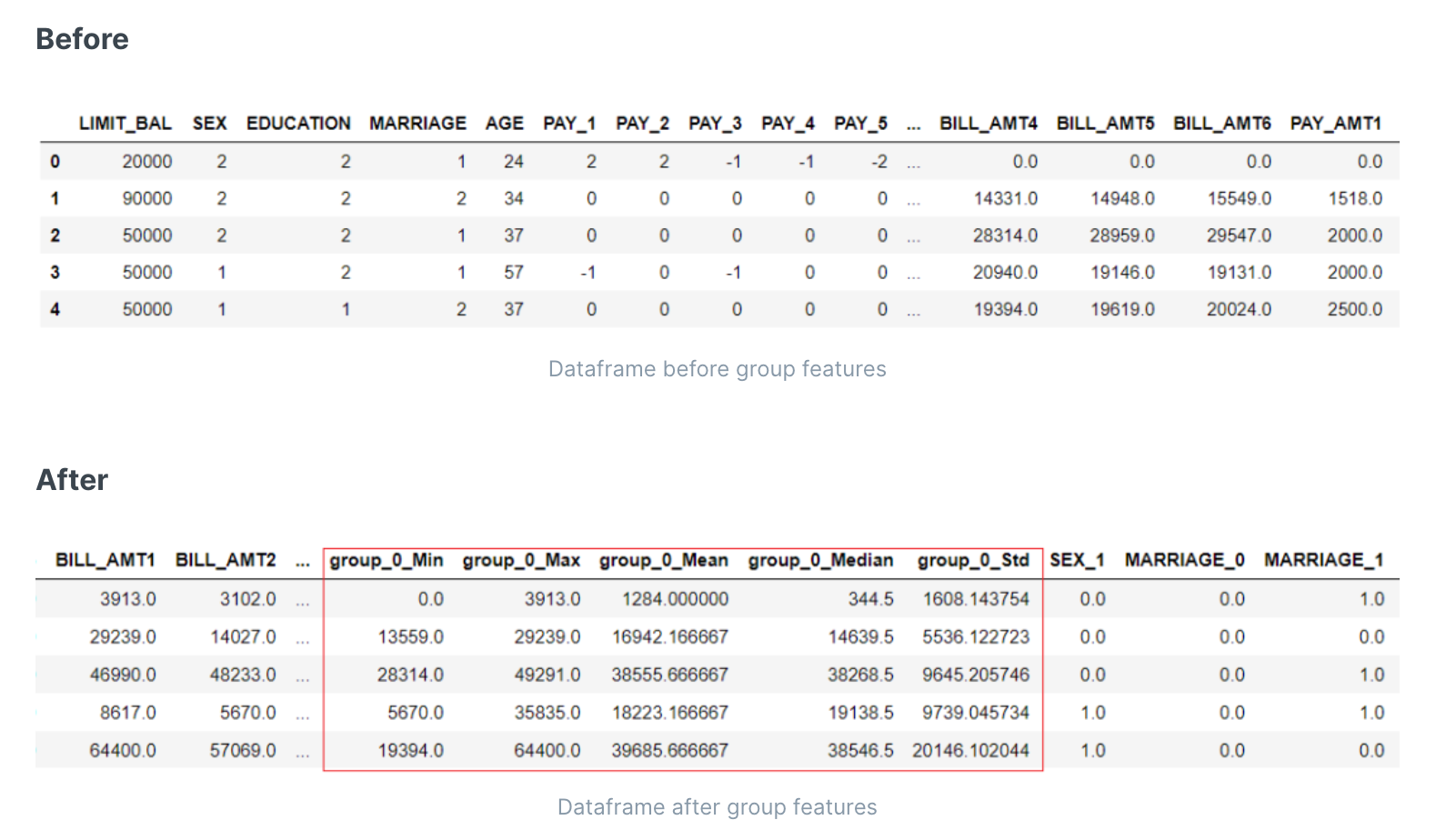
- 生成多特征聚合值(如a,b特征,生成mean([a,b])或者sum([a,b]))
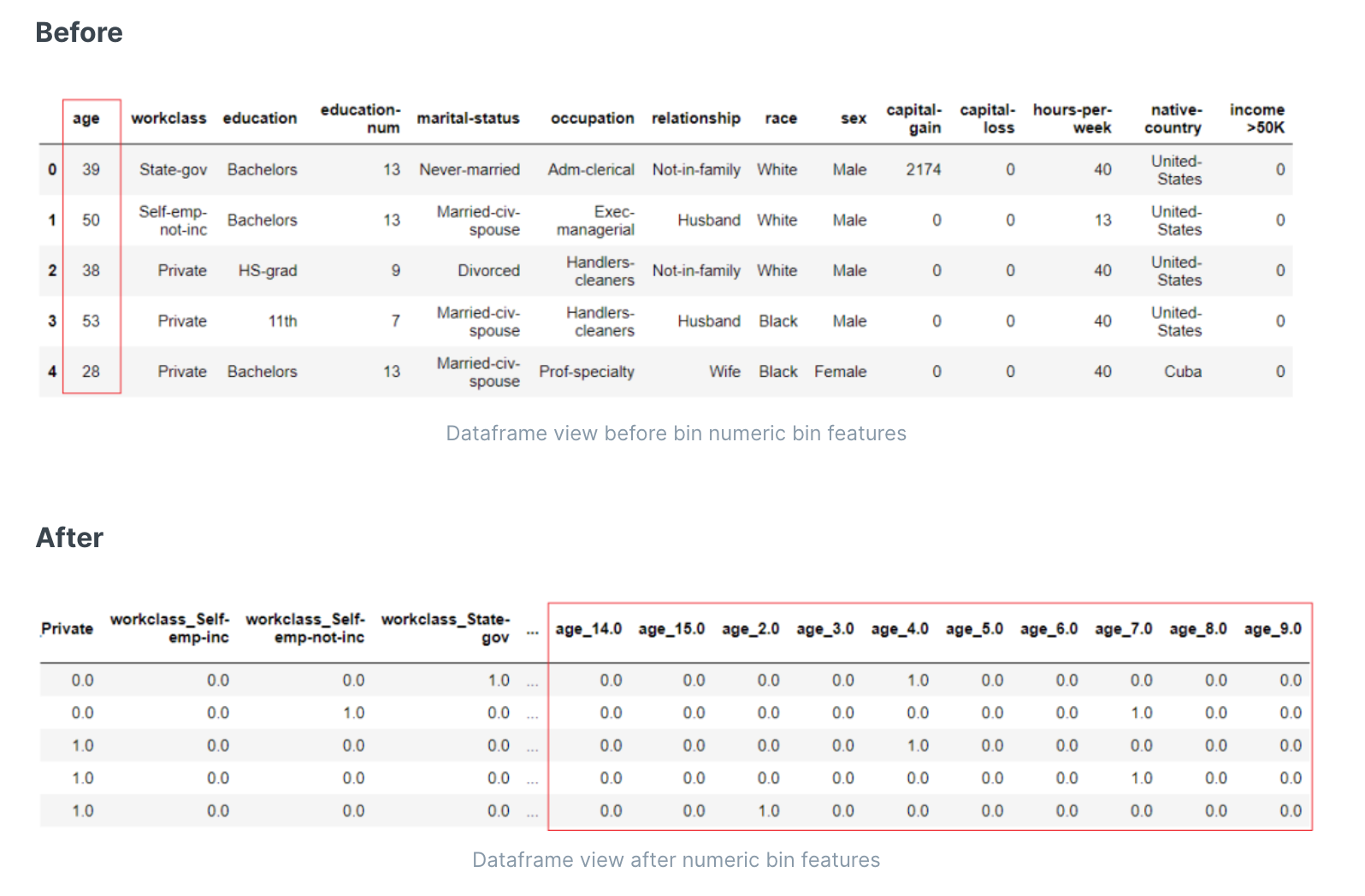
- 数值分箱
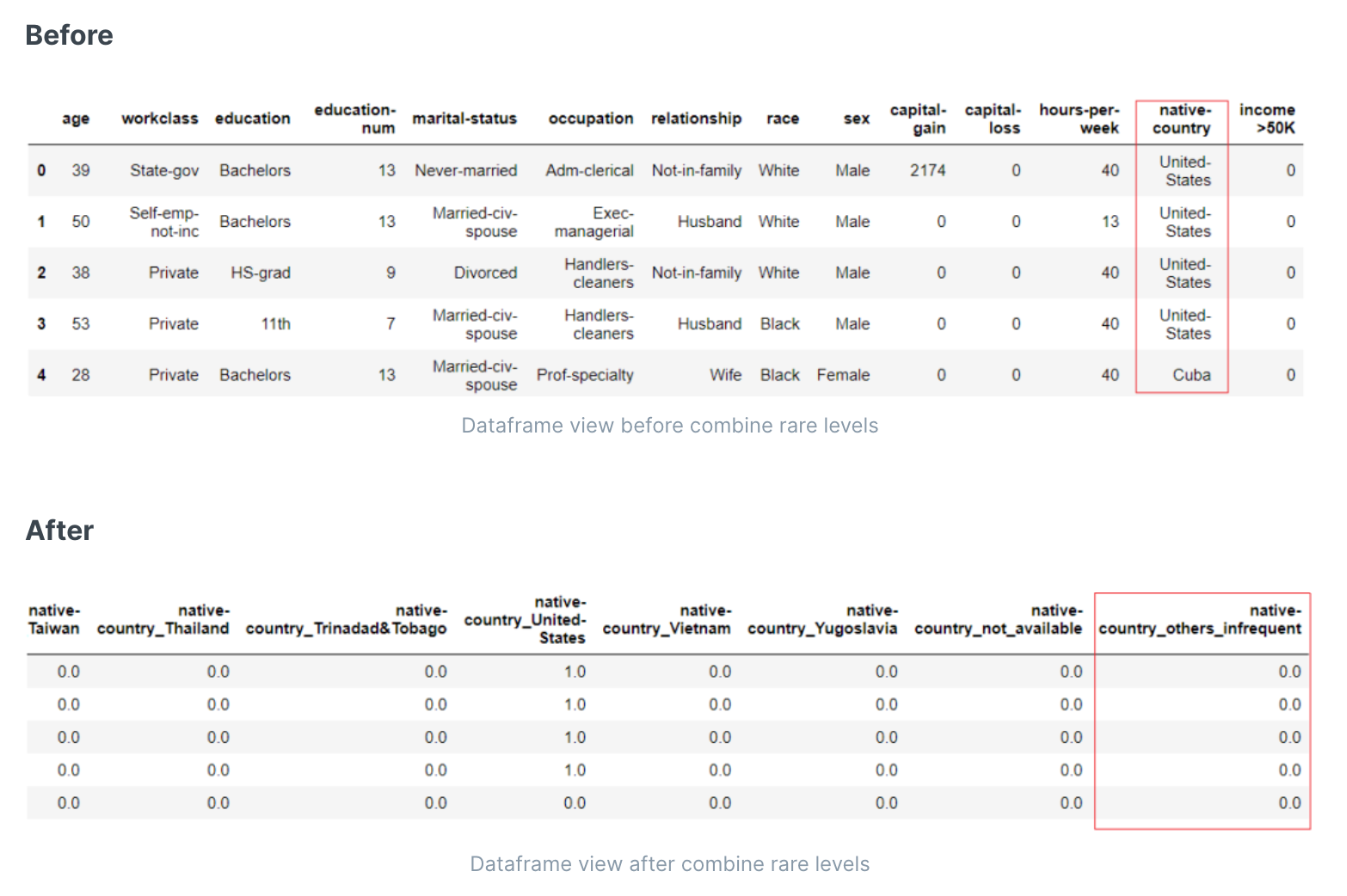
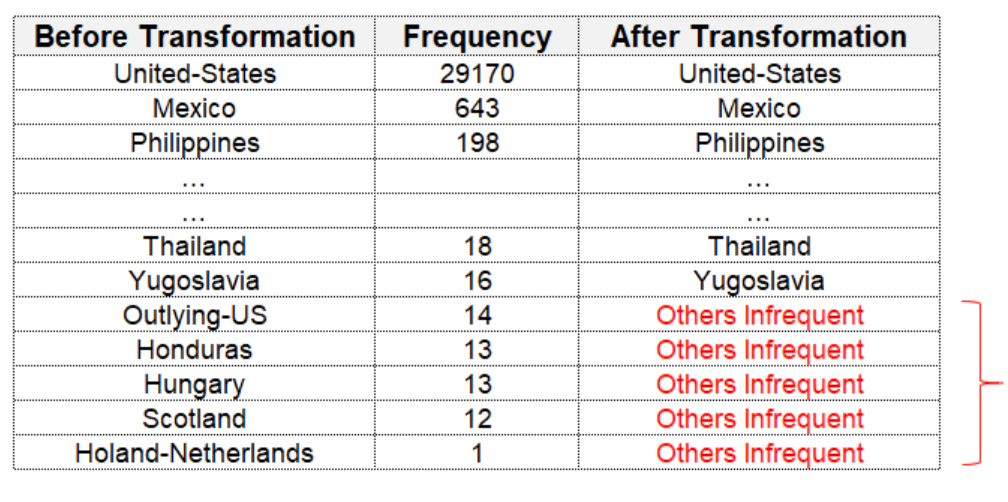
- 合并稀有值(如剩余的小部分值统称为其他)
- 特征选择
- 剔除重要度低的特征
- 随机剔除相关性极高的特征
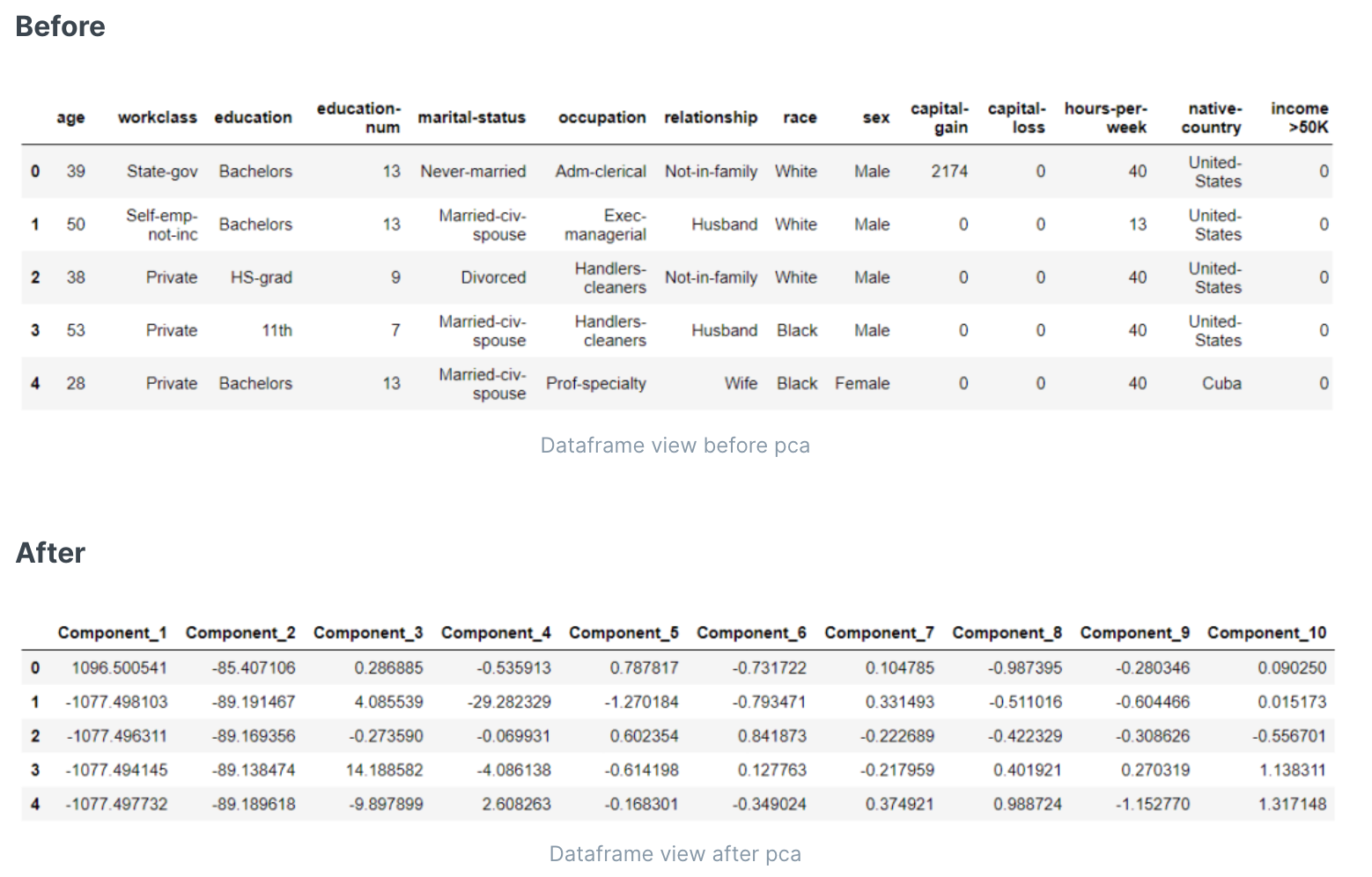
- 特征合并(主成分分析)
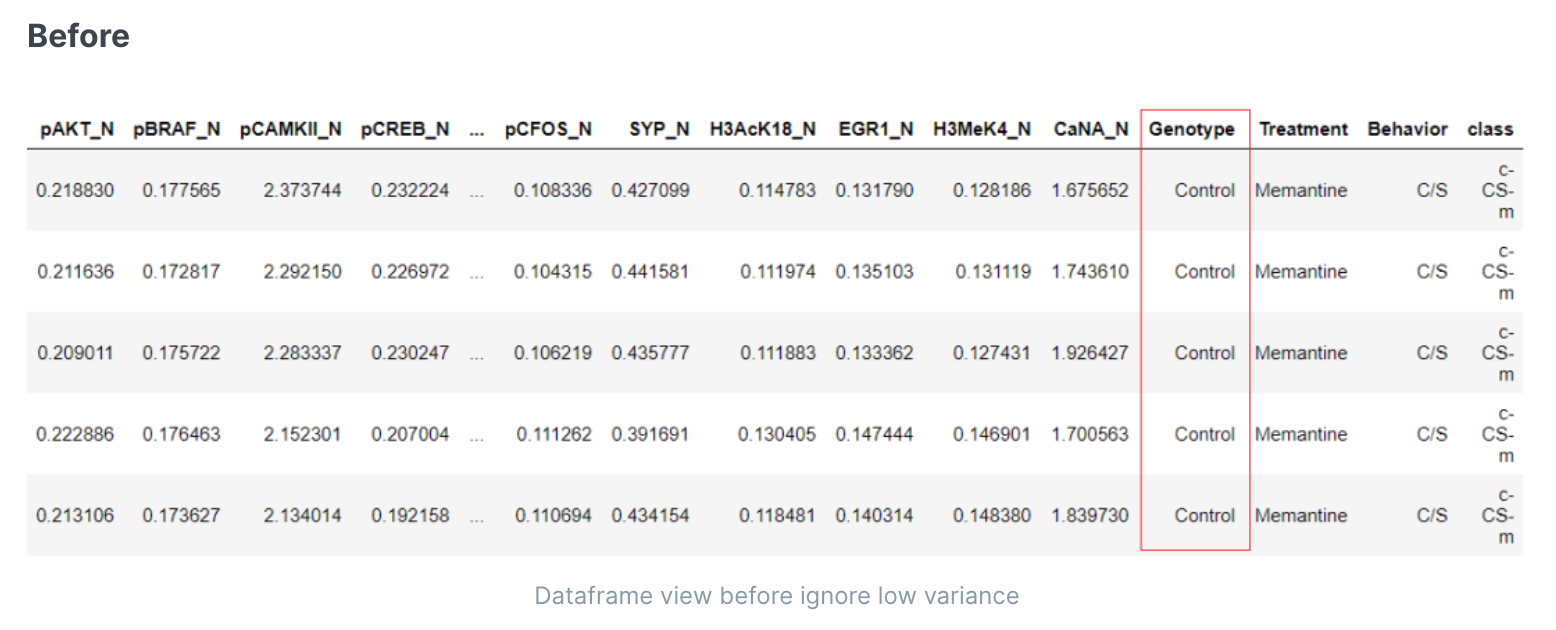
- 剔除低方差的特征(没有区分度)
- 算法选择
- 分类
- 回归
- 聚类
- 异常检测
- 时间序列
- 模型调优
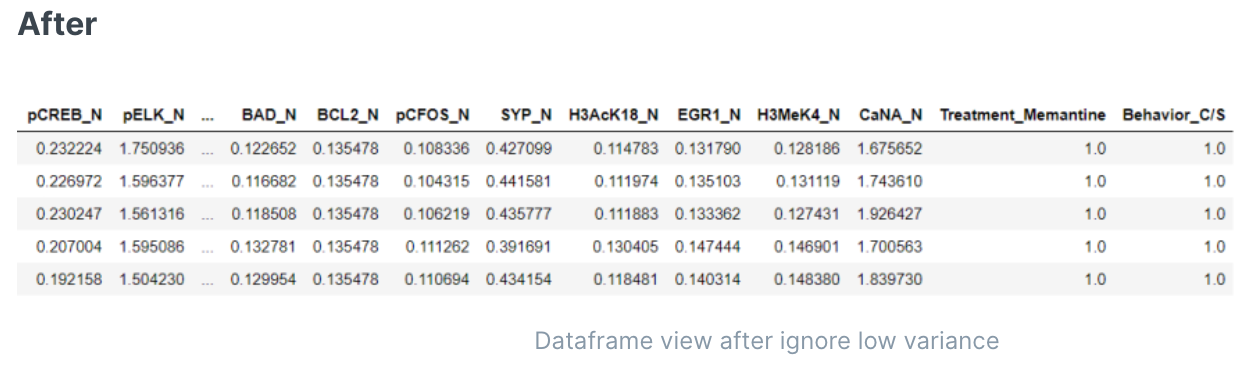
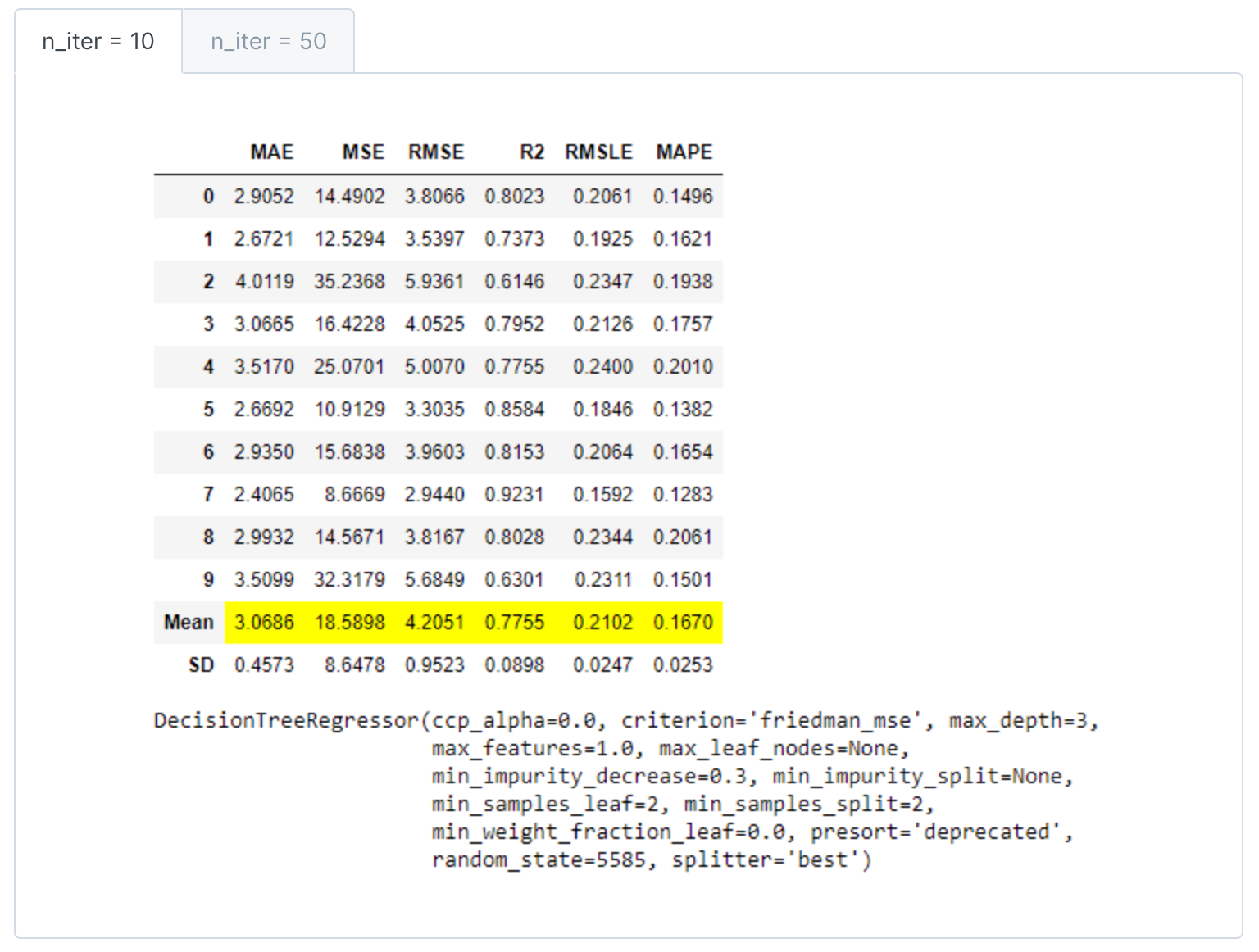
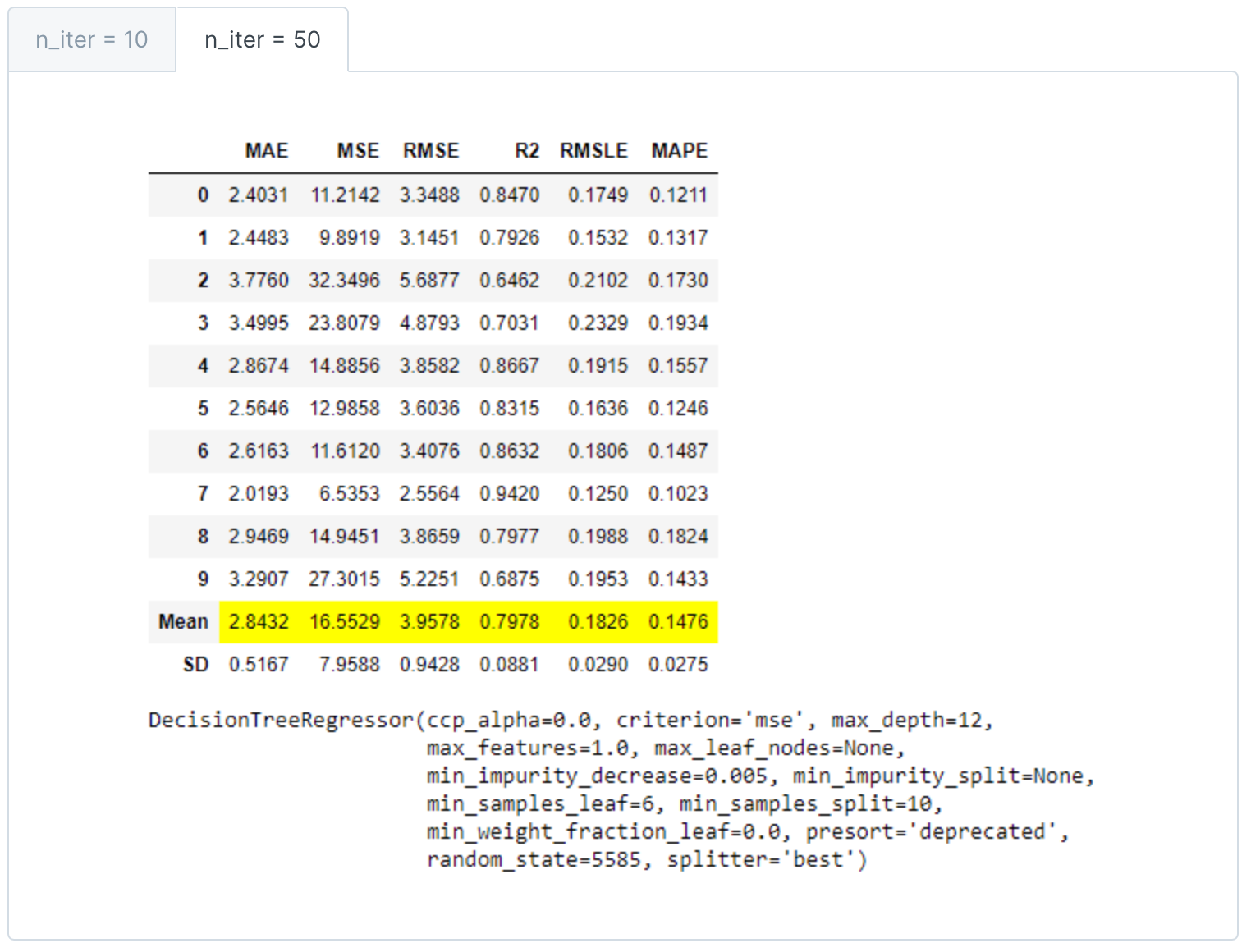
- 迭代次数调优
- 选择正确的评估指标或自定义评估指标
- 网格搜索调优
- 选择参数搜索算法调优((如随机、贝叶斯概率、 optuna、TPE或其他))
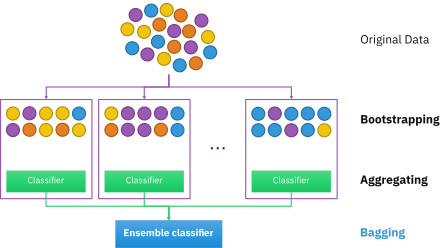
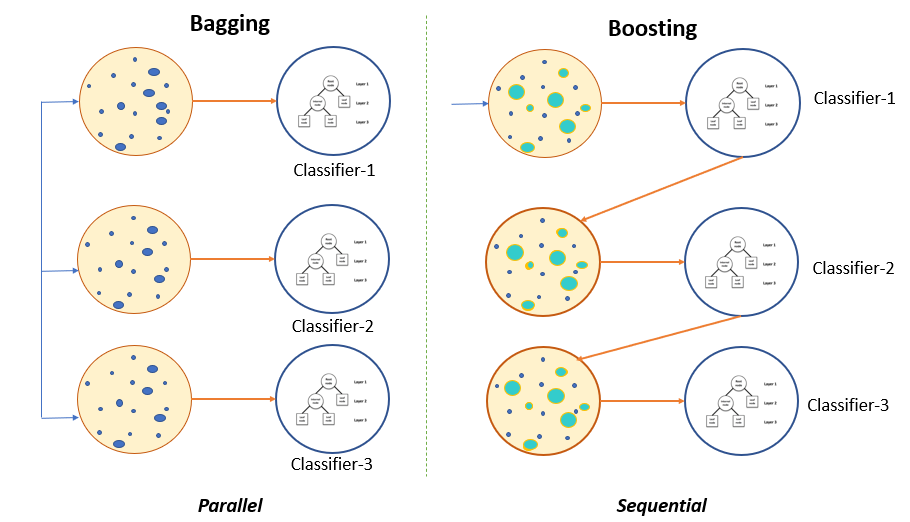
- ensemble模型调优(单模型的Bagging or Boosting)
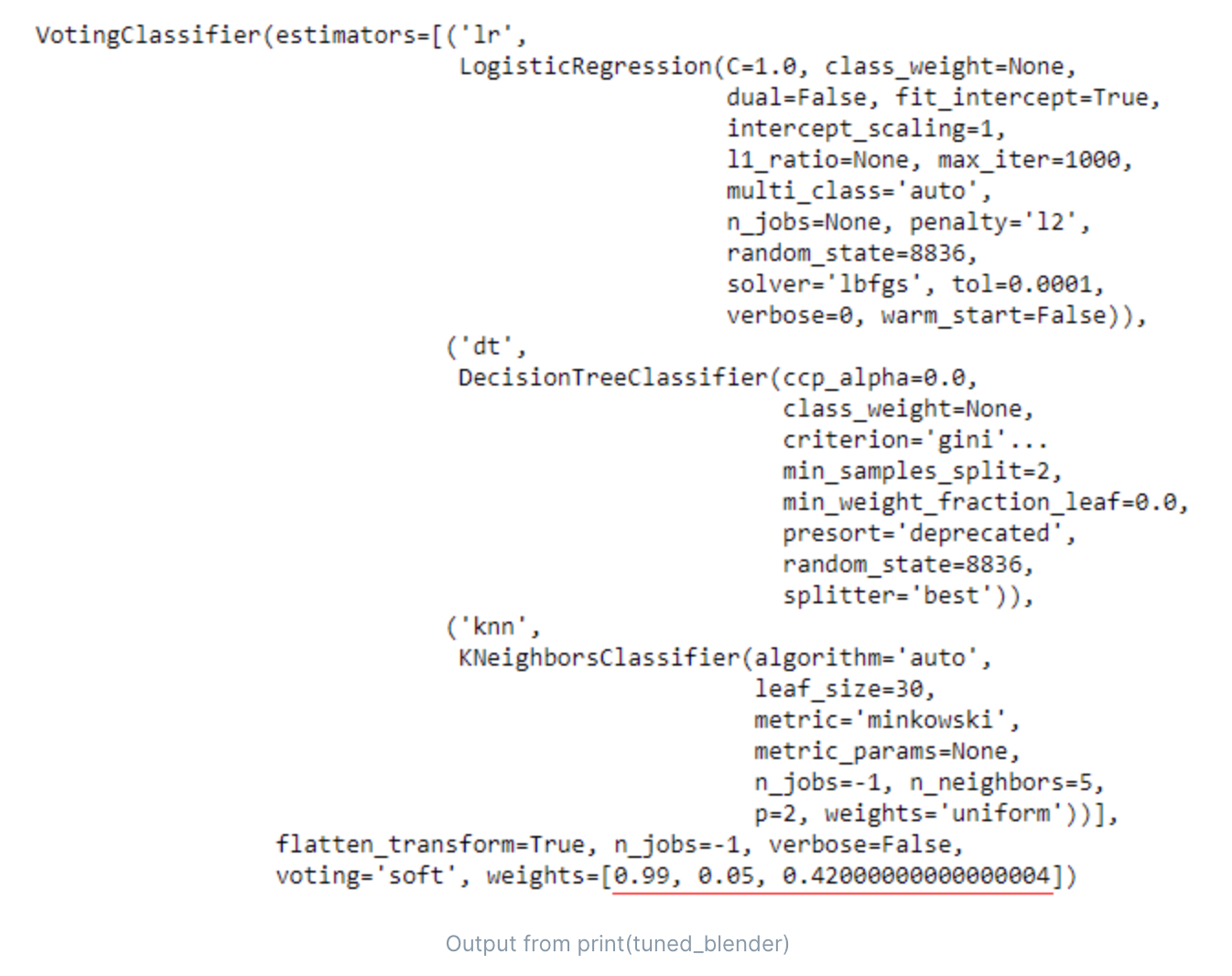
- blend模型调优(如[lr, dt, knn],进行软投票/硬投票的组合模型)
- stack模型调优(使用上个模型预测的结果,作为下个模型的输入)
- 模型评估
- 分类(auc值、准确度、召回率、精确度、mcc、kappa)
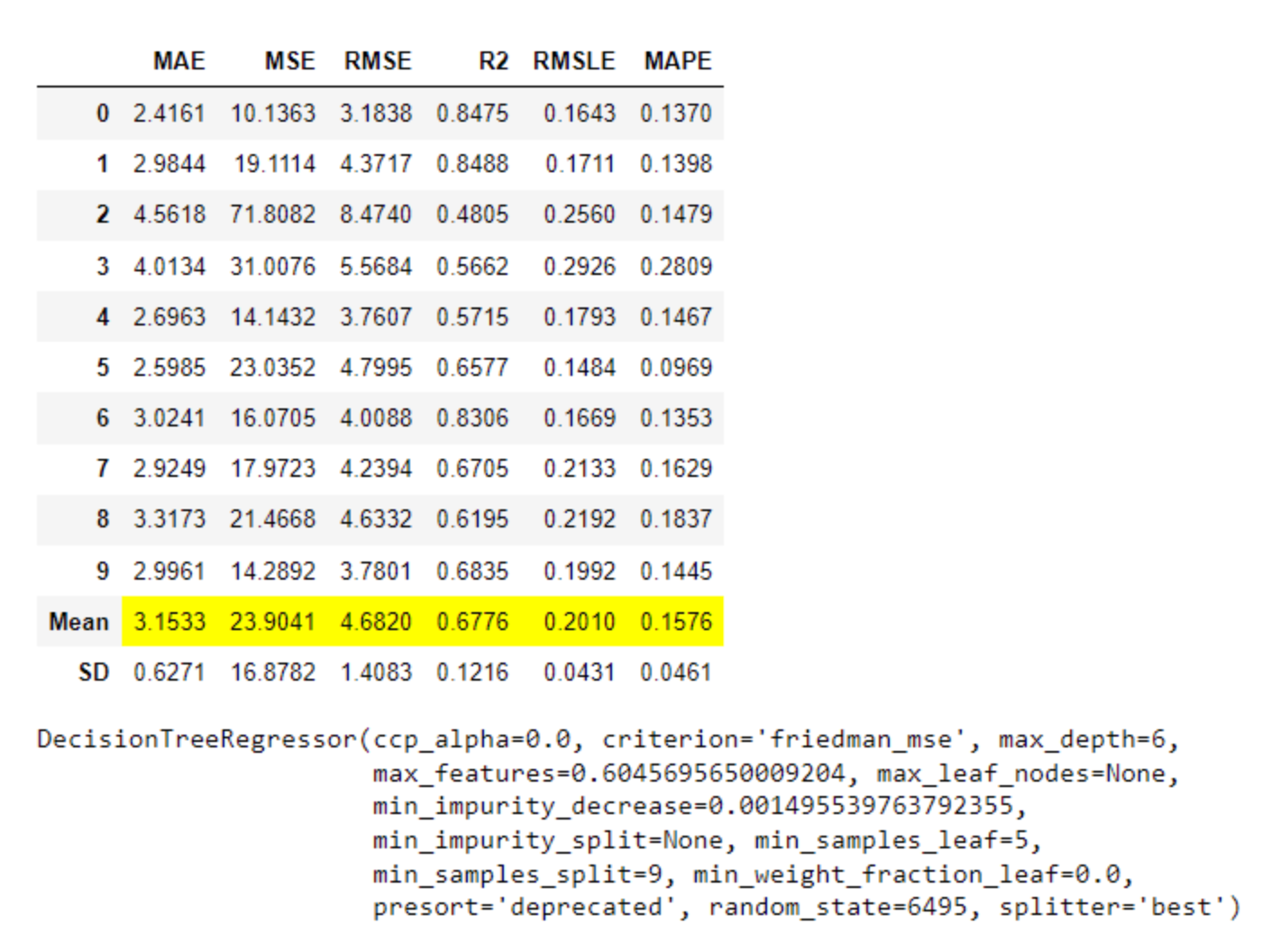
- 回归(MAE、MSE、RMSE、R2、RMSLE、MAPE)
- 聚类(Silhouette、Calinski-Harabasz、Davies-Bouldin、Homogeneity、Rand Index 、Completeness)
- 异常检测(auc值、准确度、召回率、精确度、mcc、kappa)
- 时间序列(MAE、MSE、RMSE、R2、RMSLE、MAPE、MASE)
- 自定义评估指标
- 模型解释
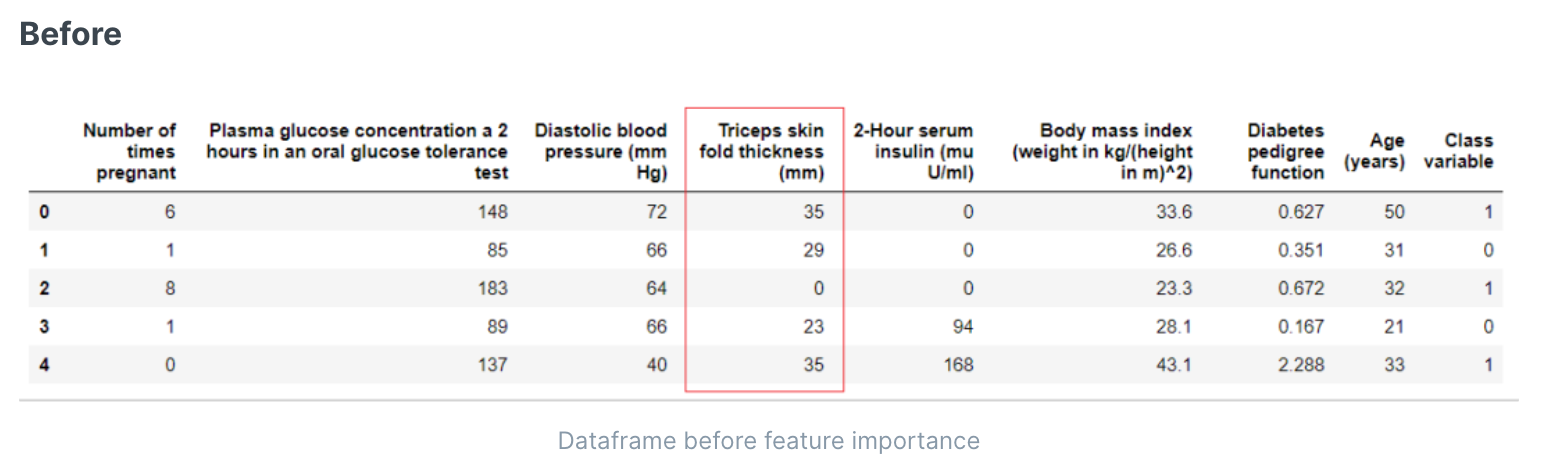
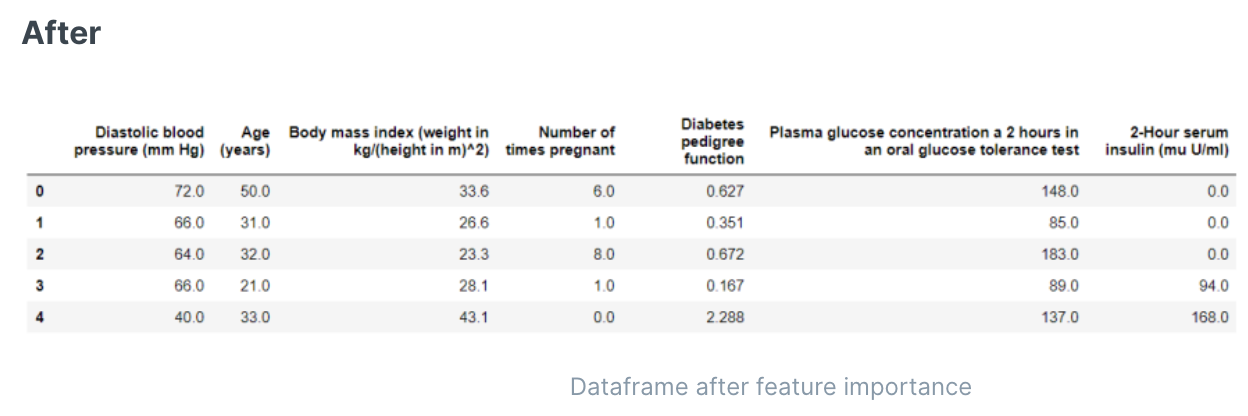
- 特征重要性排行
- SHAP依赖图
- 各特征的SHAP值
- SHAP交互值
- 模型部署
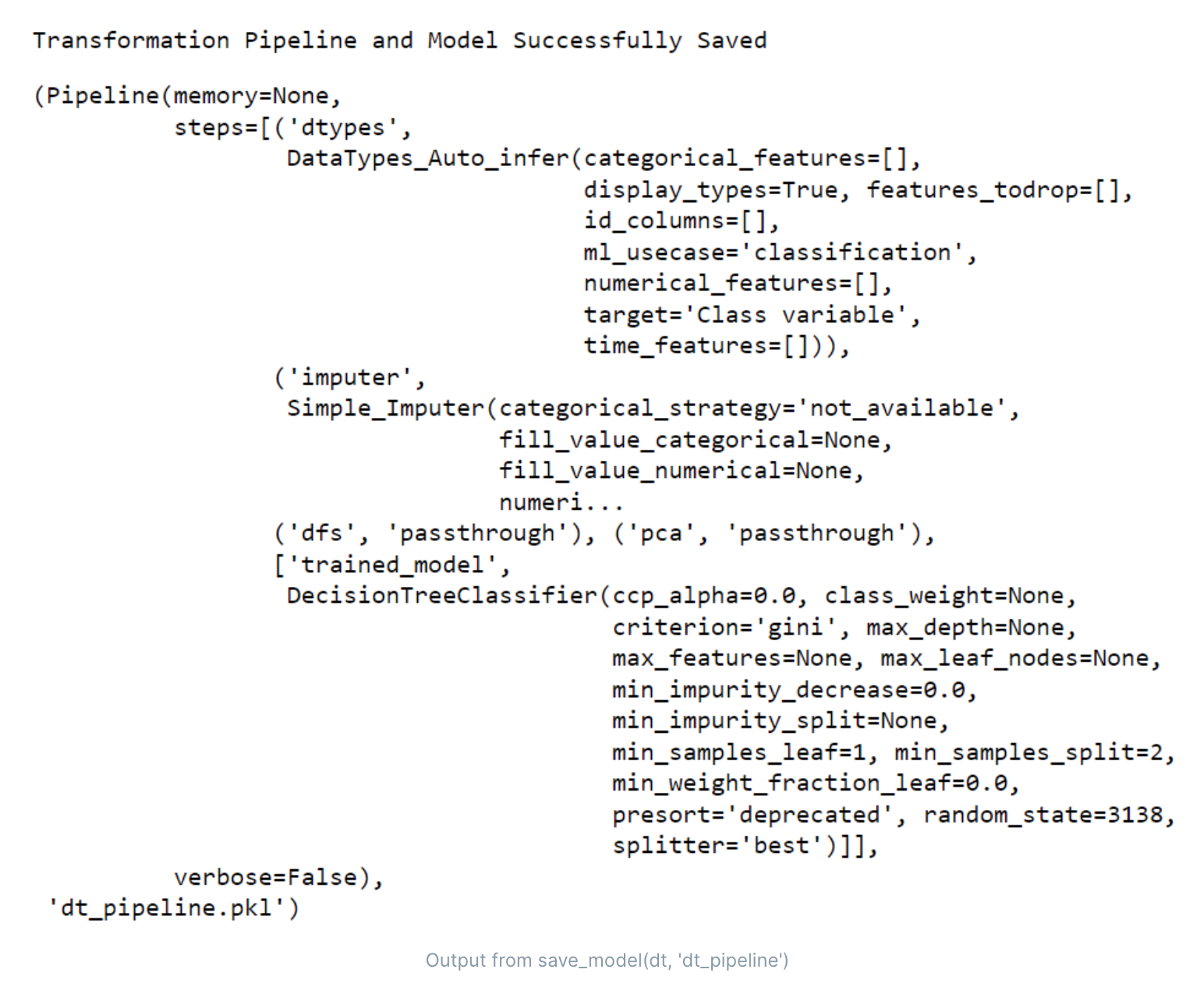
- 保存模型
- 加载模型
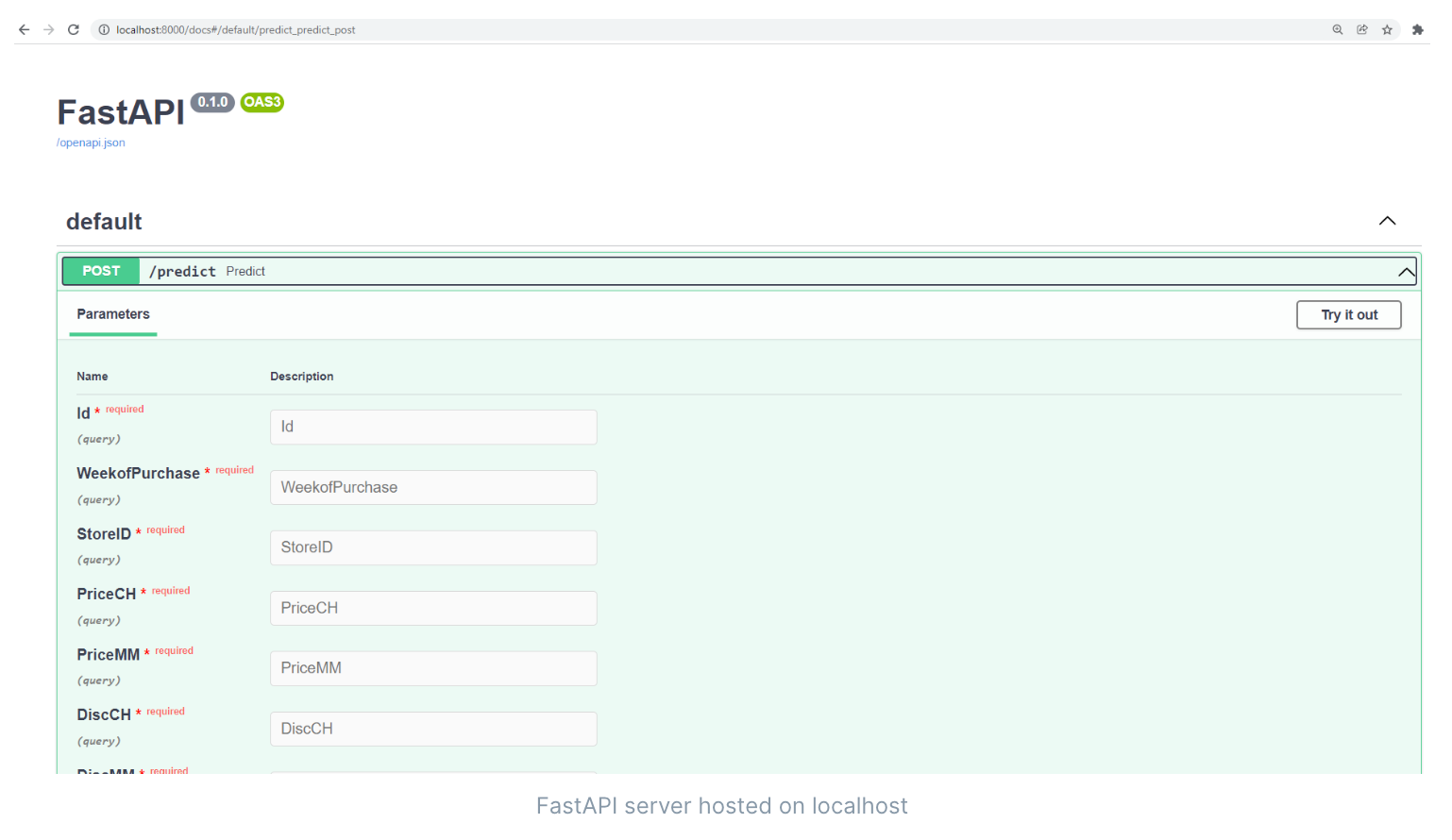
- 制作api
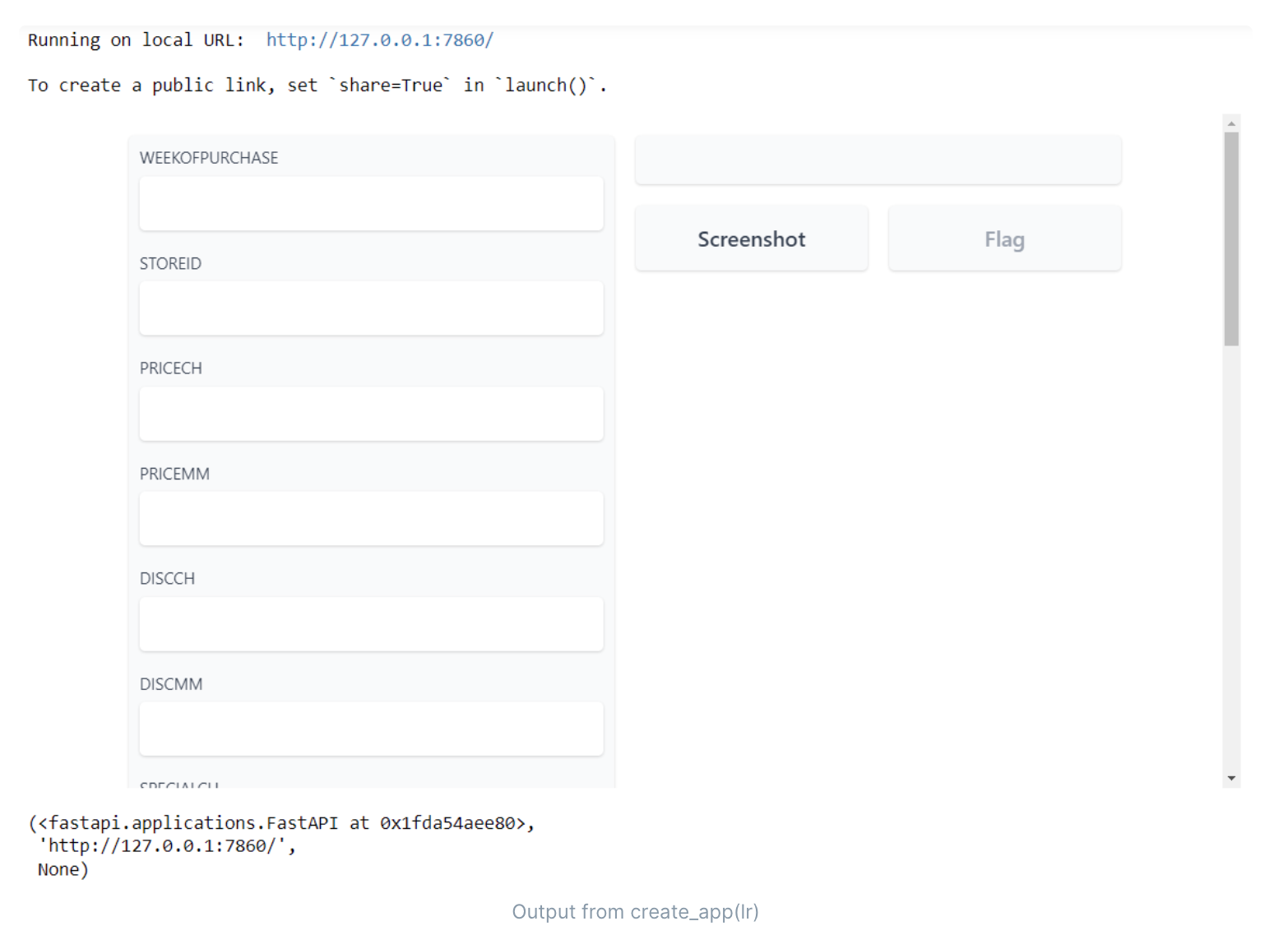
- 搭建预测页面
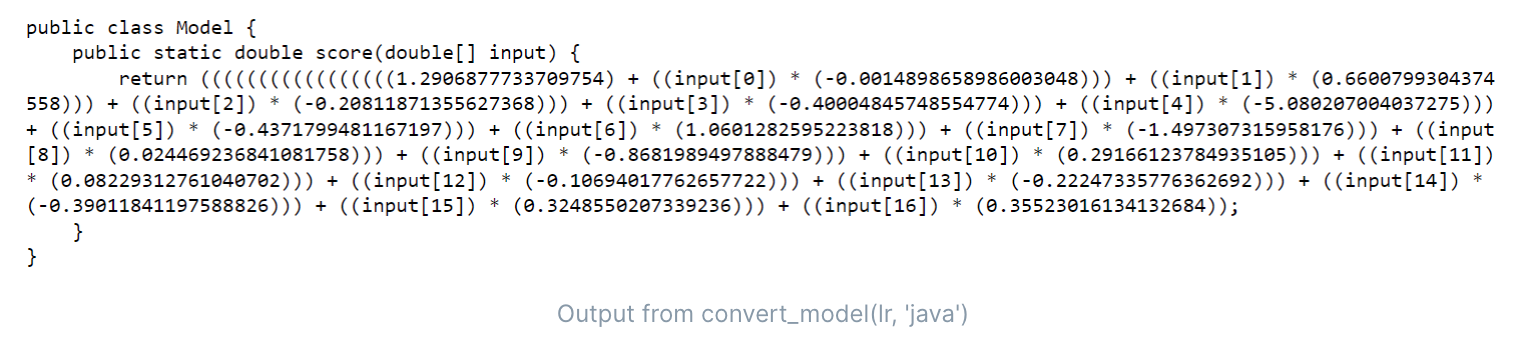
- 转换模型(java、c++)
- docker部署
- 数据获取
- 效率和成本
- 建模时间与收益
建模步骤:
数据预处理
缺失值处理
- 数值型
删除: 删除包含缺失值的行。
均值: 用列的平均值填充。
中位数: 用列的中位数填充。
众数: 用最频繁出现的值填充。
knn:使用K-近邻方法进行插补。
int或float:使用自定义数字值进行插补。
建模预测填充:使用未缺失的值进行建模,预测缺失值。
- 类别型
删除:删除包含缺失值的行。
众数:用最常见的值填充。
字符串:使用自定义的字符串填充。(如:其他)
建模预测填充:使用未缺失的值进行建模,预测缺失值。
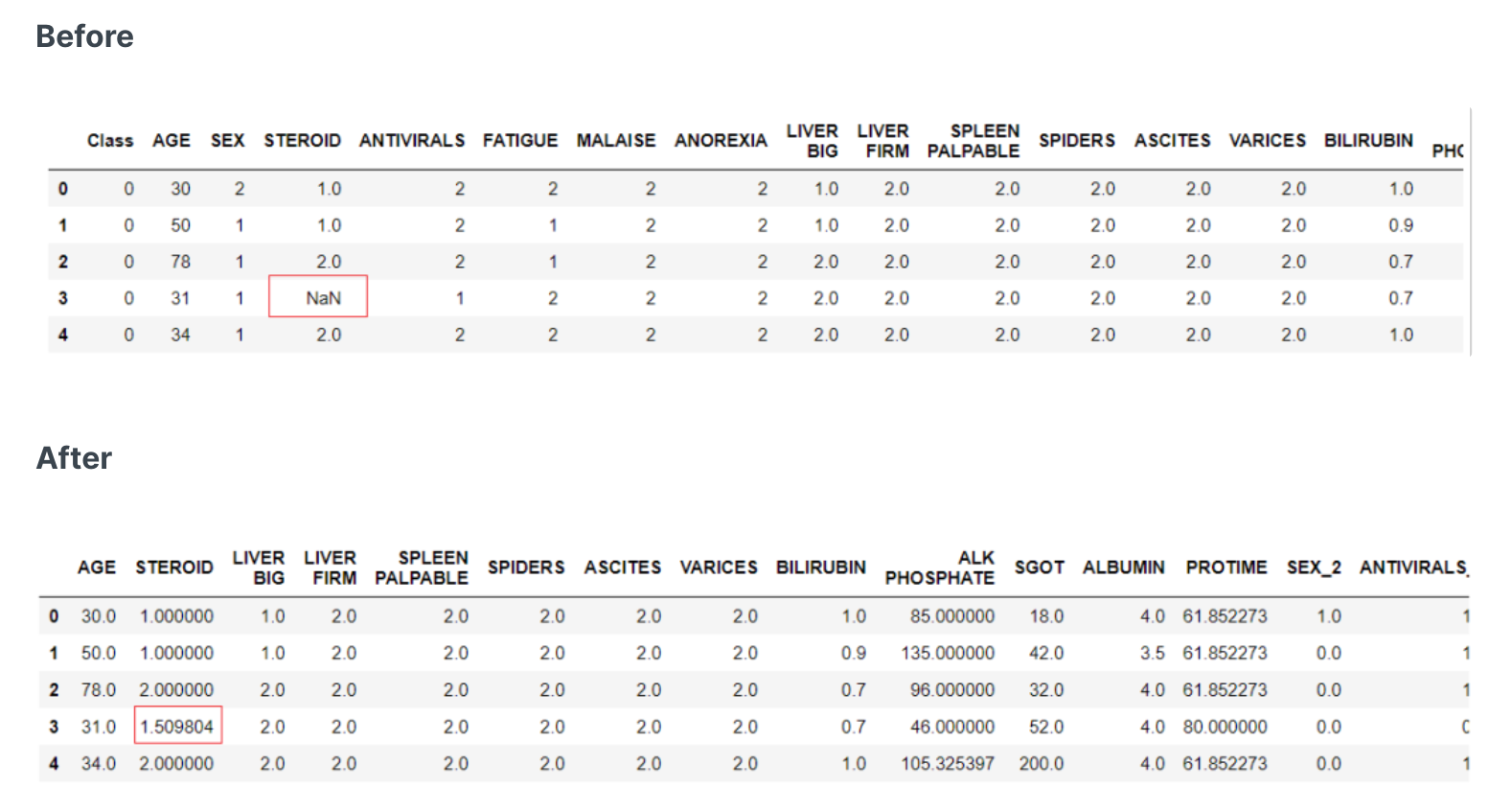
简单填充器与机器学习预测填充器的比较(明显是智能填充效果好)
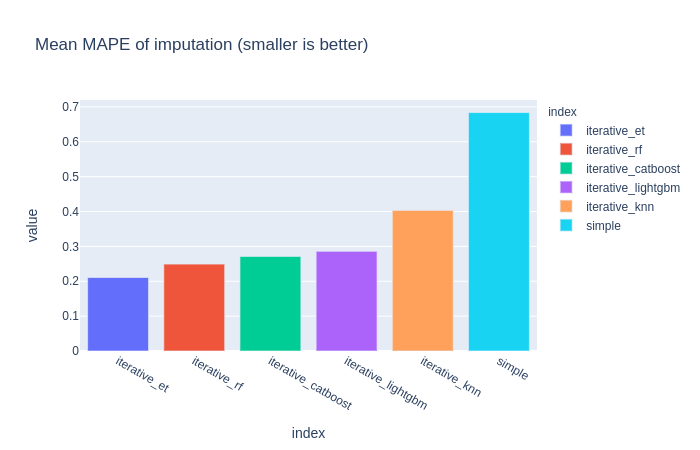 🧐MAPE 是 "Mean Absolute Percentage Error" 的缩写,中文翻译为 "平均绝对百分比误差"。它是一种衡量预测模型或者估计方法准确度的指标,主要用在回归问题中。MAPE 的计算公式如下: MAPE = (1/n) Σ ( |真实值 - 预测值| / |真实值| ) * 100% 其中,Σ 表示对所有数据求和,n 表示数据的总数量。MAPE 的值越小,说明预测模型的准确度越高。 注意,当真实值接近或等于0时,MAPE可能会变得非常大或者无法定义,这是它的一种缺点。因此,在使用 MAPE 时,你需要确保你的数据不会让这种情况发生,或者你需要对这种情况进行特殊处理。
🧐MAPE 是 "Mean Absolute Percentage Error" 的缩写,中文翻译为 "平均绝对百分比误差"。它是一种衡量预测模型或者估计方法准确度的指标,主要用在回归问题中。MAPE 的计算公式如下: MAPE = (1/n) Σ ( |真实值 - 预测值| / |真实值| ) * 100% 其中,Σ 表示对所有数据求和,n 表示数据的总数量。MAPE 的值越小,说明预测模型的准确度越高。 注意,当真实值接近或等于0时,MAPE可能会变得非常大或者无法定义,这是它的一种缺点。因此,在使用 MAPE 时,你需要确保你的数据不会让这种情况发生,或者你需要对这种情况进行特殊处理。
- 数值型
catboost编码
什么是catboost编码:
假设我们有以下数据集,其中
X是类别特征,y是目标变量(0/1分类):Index X y 1 Cat 0 2 Dog 1 3 Dog 0 4 Cat 1 5 Bird 1 我们按照索引(Index)的顺序对数据进行CatBoost编码。编码结果如下:
Index X y CatBoost Encoding 1 Cat 0 NaN 2 Dog 1 NaN 3 Dog 0 1.0 4 Cat 1 0.0 5 Bird 1 NaN 在第一行,'Cat'是第一次出现,所以我们还没有看到任何历史数据,故编码值为NaN。同样,第二行中'Dog'也是第一次出现,编码值也为NaN。
在第三行,'Dog'出现了第二次,这时候我们可以看到它之前的历史数据(在第二行中),对应的目标值是1,所以这里的编码值就是1。
在第四行,'Cat'出现了第二次,其历史数据(在第一行中)对应的目标值是0,所以编码值就是0。
最后,在第五行,'Bird'是第一次出现,编码值仍然是NaN。
这样,我们就得到了CatBoost编码的结果。在实际使用中,我们会用一些策略来处理第一次出现的类别值(比如用全局平均值来填充)。
另外,对于使用CatBoost编码的机器学习模型来说,它看到的是编码后的值,而不是原始的类别标签,这使得模型能够从这些数值中捕捉到更多的信息。
Target编码
目标编码(也被称为平均编码、响应编码、或者是基于目标的编码)是一种处理分类特征的方法,特别是那些有高基数(即很多唯一值)的特征。这是一种非常有效的技巧,尤其是在处理树形模型(如决策树和随机森林)时。
目标编码涉及使用目标变量(响应变量)的平均值来替代每个类别的值。例如,如果你有一个二元分类问题,并且你的目标编码的特征是"颜色",其可能的值为"红色"、"蓝色"和"绿色",那么每一个颜色将被它对应的目标变量的平均值所替换。如果"红色"的目标平均值为0.8,"蓝色"的为0.5,"绿色"的为0.3,那么目标编码将会替换这些颜色为这些平均值。
目标编码的一个优点是它可以帮助模型利用类别特征和目标变量之间的关系。然而,这种方法的缺点是,它可能会引入目标泄露,即模型可能会看到在训练过程中不应该看到的信息。这可能会导致模型在训练数据上过拟合,但在新的、未见过的数据上表现不佳。因此,在使用目标编码时,我们需要仔细进行交叉验证,或者使用一些技巧来防止目标泄露,例如"平滑"(在目标编码中引入一些噪声)或者"K-Fold"目标编码(在K-Fold交叉验证的每一折中都重新进行目标编码)。
在某些场景下,目标编码能够有效提高模型的表现,尤其是在处理具有高基数分类特征的问题时。然而,它需要谨慎使用,以避免过拟合和目标泄露的问题。
举个例子:
假设我们有一个数据集,包括一个分类特征("城市")和一个二元目标特征("购买" - 表示人们是否购买了某个产品):
城市 购买 北京 1 北京 0 北京 1 上海 1 上海 1 广州 0 广州 0 广州 0 广州 1 我们可以计算每个城市的"购买"平均值,然后用这个平均值来替换原始的城市名称。在上面的例子中,"北京"的平均值是 (1+0+1)/3 = 0.67,"上海"的平均值是 (1+1)/2 = 1.0,"广州"的平均值是 (0+0+0+1)/4 = 0.25。所以替换后的数据如下:
城市 购买 0.67 1 0.67 0 0.67 1 1.0 1 1.0 1 0.25 0 0.25 0 0.25 0 0.25 1 注意到,现在的"城市"列已经从分类变量转变为了数值变量,这样就可以在各种机器学习模型中使用了。同时,这种转变捕获了"城市"特征与目标"购买"之间的某种关系:例如,上海的平均购买率较高,这种信息可能对预测其他上海数据点是否购买有帮助。
但是,这种方法要小心防止过拟合和数据泄漏。在实践中,我们通常不会在整个数据集上进行这种转换,而是在交叉验证的训练集上进行,然后应用到验证集和测试集。这样可以保证我们的模型不会接触到在训练阶段不应该了解的信息。
sum编码
Sum编码,也被称为Deviation编码或Effect编码,是一种独热编码的变体。它用于分类特征的编码,并且经常用于线性回归、逻辑回归等模型。
与独热编码不同,Sum编码不会产生完全冗余的特征。在独热编码中,如果一个分类特征有k个不同的类别,那么会产生k个新的二进制特征,这些特征之间是完全冗余的,也就是说,你可以通过其他k-1个特征推断出第k个特征。然而,Sum编码只会产生k-1个新的二进制特征。
在Sum编码中,每个类别被赋予一个二进制编码,其中一个类别(通常是最后一个,但也可以是任何一个)的编码是所有-1(而不是0,如在独热编码中),其他类别的编码是一个由1和0组成的向量。每个类别的编码值都相对于最后一个类别(其编码值为-1)。
例如,如果你有一个特征,它有三个类别'A','B'和'C'。在Sum编码中,这些类别可能会被编码为:
- A: 1, 0
- B: 0, 1
- C: -1, -1
Sum编码的一个主要优点是它可以处理分类特征中的线性趋势。然而,一个主要的缺点是它的编码方案不稳定,即对类别的一个小的重排序可能会导致编码的显著改变。此外,如果数据中有未在训练数据中出现的新类别,Sum编码可能会产生问题。
举个例子:
假设我们有一个名为“颜色”的分类特征,其中包含三个类别:“红色”、“蓝色”和“绿色”。
在Sum编码中,我们会为“红色”和“蓝色”分配编码,而“绿色”将被认为是基线类别,其编码为-1。
例如:
- "红色": 1, 0
- "蓝色": 0, 1
- "绿色": -1, -1
在这种情况下,原始数据可能如下:
颜色
红色
蓝色
绿色
红色
绿色
蓝色
编码后的数据会是:
颜色_1 颜色_2 1 0 0 1 -1 -1 1 0 -1 -1 0 1 注意,Sum编码中的每一列都相对于“绿色”(被选为基线类别)进行编码。例如,第一列对应于“红色”相对于“绿色”的效果,第二列对应于“蓝色”相对于“绿色”的效果。
留一法编码
“留一法编码”(Leave One Out Encoding)也称为“留一法目标编码”,它是一种将类别特征转换为数值的编码方式,常用于机器学习中的特征工程。
这种方法主要用于处理类别特征(categorical features),其主要步骤如下:
- 选择一个类别特征。
- 对于每一个类别,我们计算所有其他样本中该类别的目标变量的平均值(“留一法”就在此,我们不包括当前样本的目标值)。
这种方法的优点是可以引入目标变量的信息,但缺点是可能引入过拟合,因为这种方法直接使用了目标变量的信息。所以在使用时,通常会结合交叉验证(cross-validation)等方法来减少过拟合。
假设我们有以下数据:
类别 目标 A 1 B 0 A 0 A 1 B 1 B 0 对应的“留一法编码”为:
类别 目标 编码 A 1 0.5 B 0 0.5 A 0 1.0 A 1 0.5 B 1 0.0 B 0 0.5 其中,每一行的编码都是在除了当前行之外的其他行中,相同类别的目标的平均值。例如,第一行的“编码”值是在除了第一行之外的其他行中,类别为“A”的目标的平均值((0+1)/2 = 0.5)。
我们来通过一个简单的例子来解释一下留一法编码(Leave One Out Encoding)。
首先,我们有一个简单的数据集如下:
ID 类别特征 目标变量 1 A 1 2 B 0 3 A 0 4 B 1 5 A 1 6 B 0 我们要对“类别特征”进行留一法编码。根据留一法编码的定义,每个样本的编码值为除自身外同类别的样本的目标变量的平均值。所以我们可以得到如下的编码结果:
ID 类别特征 目标变量 留一法编码 1 A 1 (0+1)/2 = 0.5 2 B 0 (1+0)/2 = 0.5 3 A 0 (1+1)/2 = 1.0 4 B 1 (0+0)/2 = 0.0 5 A 1 (1+0)/2 = 0.5 6 B 0 (0+1)/2 = 0.5 例如,对于ID为1的样本,其类别特征为“A”,在除去它之外的其他“A”类别的样本的目标变量的平均值为(0+1)/2 = 0.5,所以其留一法编码值为0.5。
这样,我们就完成了“类别特征”的留一法编码。
特征标准化
进行特征标准化的原因是消除不同特征之间的量纲(scale)差异,使得所有特征都在同样的范围内。这在许多机器学习算法中是非常重要的,尤其是那些对特征的范围和分布敏感的算法,如支持向量机(SVM)、K-近邻(KNN)和梯度下降等。
常用方法:
- z-score :标准化计算公式为 z = (x - u) / s
- minmax :将每个特征单独缩放和平移,使其在 0-1 范围内。
- maxabs : 将每个特征单独缩放和平移,使得每个特征的最大绝对值为 1.0。它不会移动/居中数据,因此不会破坏任何稀疏性。
- robust :根据四分位距来缩放和平移每个特征。当数据集包含异常值时,鲁棒标度器通常可以获得更好的结果。
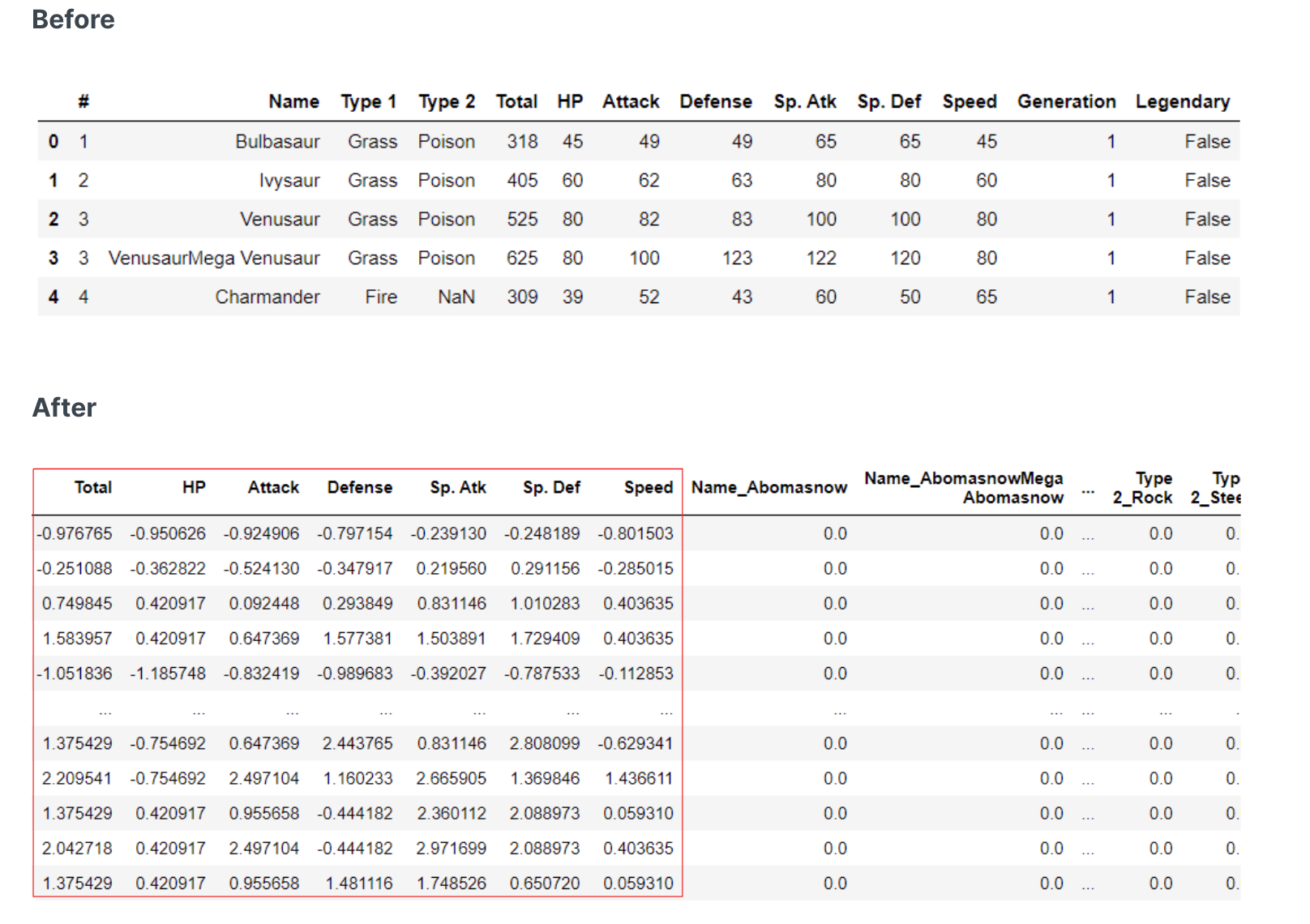
标准化的分布:
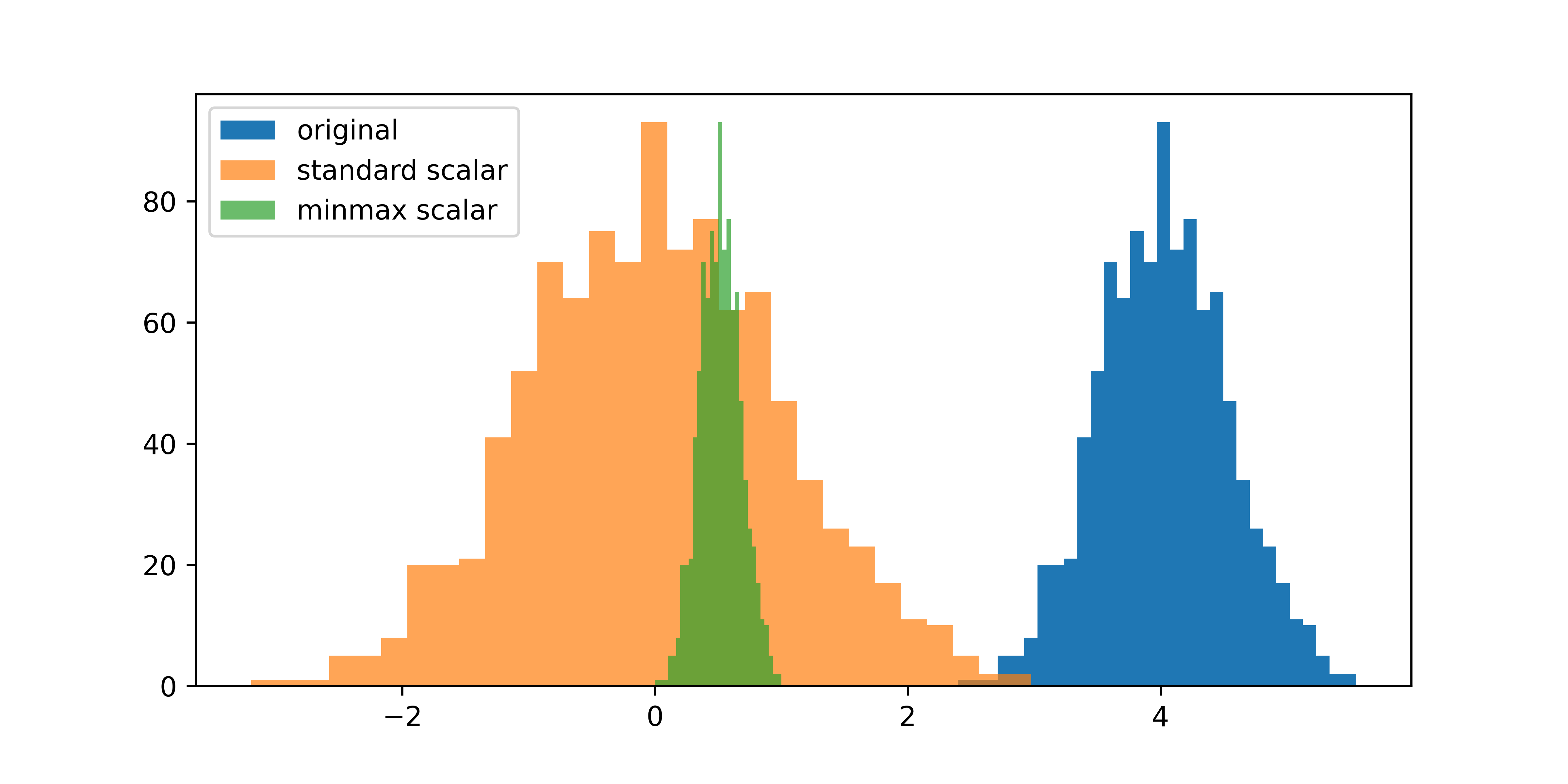
特征变换
- 数据标准化(Normalization):标准化通常指的是将数据缩放到一个固定的范围(如0到1,或者-1到1),或者将数据转换为具有0均值和1标准差的标准正态分布。这样做的目的是消除不同特征之间的量纲(scale)差异,使得所有特征都在同样的范围内。这在许多机器学习算法中是非常重要的,尤其是那些对特征的范围和分布敏感的算法,如支持向量机(SVM)、K-近邻(KNN)和梯度下降等。
- 特征转换(Feature Transformation):特征转换是一种更一般的概念,它包括标准化,但也包括更多的操作。特征转换的目标是改变数据的分布或者关系,以使其更适合特定的机器学习算法。除了标准化,其他常见的特征转换包括对数转换、平方根转换、指数转换、离散化(binning)、多项式转换等。这些转换可以处理偏态分布、非线性关系、离群值等问题,从而提高模型的性能。
虽然标准化可以重新调整数据的范围,以减少方差中数量级的影响,但特征转换是一种更激进的技术。转换改变分布的形状,使得经过转换后的数据可以用正态或近似正态分布来表示。有两种可用于转换的方法:yeo-johnson和quantile。
这两种变换都将特征集转换为遵循高斯或正态分布的形式。分位数变换是非线性的,可能会扭曲在同一比例尺上测量的变量之间的线性相关性。
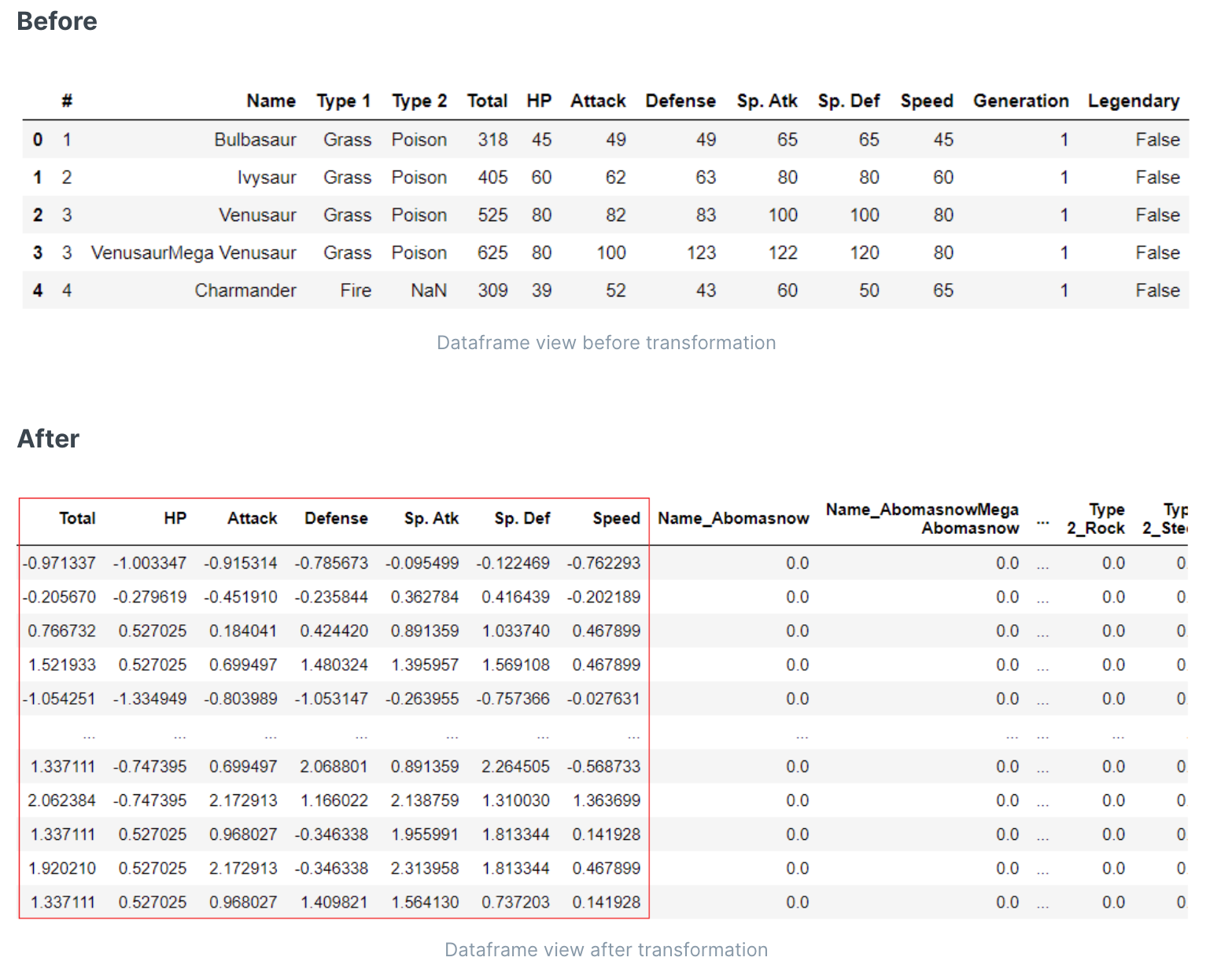
特征转换的影响:
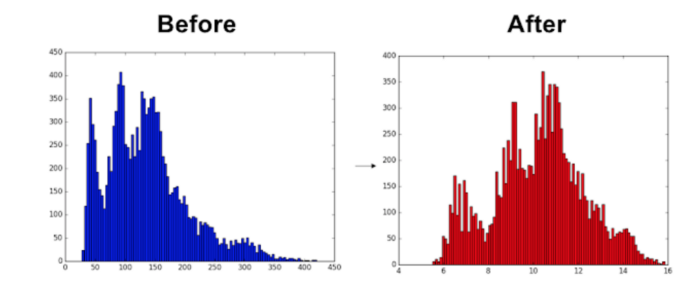
特征工程
特征选择
算法选择
分类
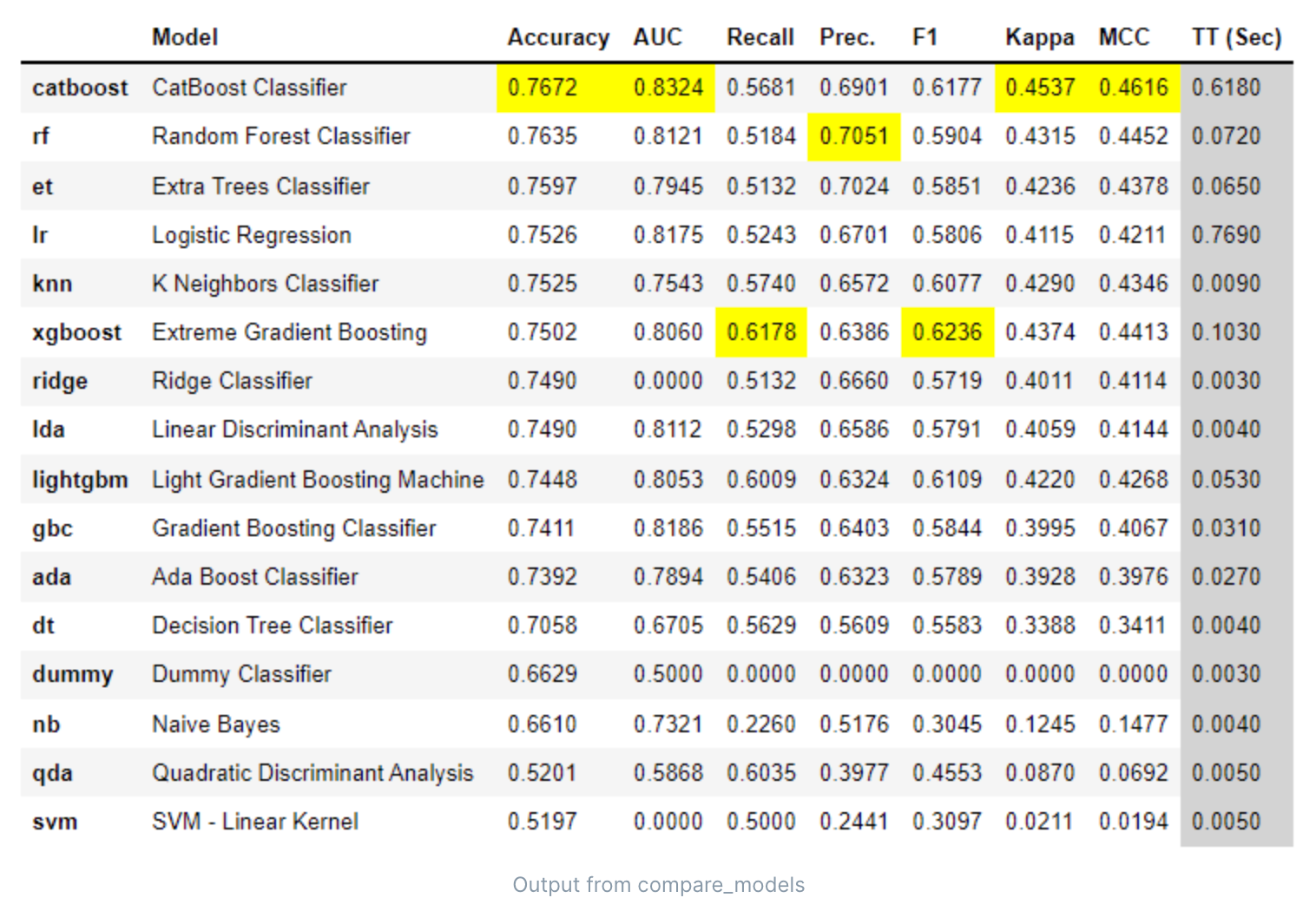
- Logistic Regression (Ir):逻辑回归是一种用于二元分类问题的统计模型。它使用逻辑函数将线性回归的输出转换为概率,这个概率可以用来预测类别。
- Ridge Classifier (ridge):Ridge 分类器是一种用于分类问题的线性模型。它通过在损失函数中添加一个 L2 正则化项(即权重的平方和)来防止过拟合。
- Linear Discriminant Analysis (Ida):线性判别分析是一种分类算法,它找到一个线性组合的特征,这些特征最大化了类别之间的方差并最小化了类别内的方差。
- Random Forest Classifier (rf):随机森林是一种集成学习方法,它通过结合多个决策树的预测结果来提高预测的准确性和稳定性。
- Naive Bayes (nb):朴素贝叶斯是一种基于贝叶斯定理的分类算法,它假设特征之间是独立的。
- CatBoost Classifier (catboost):CatBoost 是一种基于梯度提升的机器学习算法,它特别适合处理分类和回归任务中的类别特征。
- Gradient Boosting Classifier (gbc):梯度提升分类器是一种集成学习方法,它通过结合多个弱预测模型(通常是决策树)来提高预测的准确性。
- Ada Boost Classifier (ada):AdaBoost 是一种自适应的提升方法,它通过在每一轮中增加之前分类错误的样本的权重来提高预测的准确性。
- Extra Trees Classifier (et):Extra Trees 分类器是一种随机森林的变体,它在构建决策树时使用了更多的随机性。
- Quadratic Discriminant Analysis (qda):二次判别分析是一种分类算法,它假设每个类别的数据都符合多元高斯分布,并且每个类别的协方差矩阵都不同。
- Light Gradient Boosting Machine (lightgbm):LightGBM 是一种基于梯度提升的机器学习算法,它比传统的 GBDT 更快,内存使用更少,准确率更高。
- K Neighbors Classifier (knn):K 最近邻分类器是一种基于实例的学习,它根据输入样本的 k 个最近邻居的类别来预测输入样本的类别。
- Decision Tree Classifier (dt):决策树分类器是一种简单的分类算法,它通过一系列的问题来预测输入样本的类别。
- Extreme Gradient Boosting (xgboost):XGBoost 是一种优化的分布式梯度提升库,旨在实现高效,灵活和便携。它在许多机器学习竞赛中都取得了优秀的成绩。
- Dummy Classifier (dummy):Dummy 分类器不是真正的分类器,它只是简单地使用规则来预测类别,例如,总是预测最常见的类别。它通常用作基准来比较其他真正的分类器的性能。
- SVM Linear Kernel (svm):支持向量机(SVM)是一种强大的分类算法,它在高维空间中找到一个超平面来分隔不同的类别。线性核 SVM 是 SVM 的一种特殊情况,其中超平面是线性的。
回归
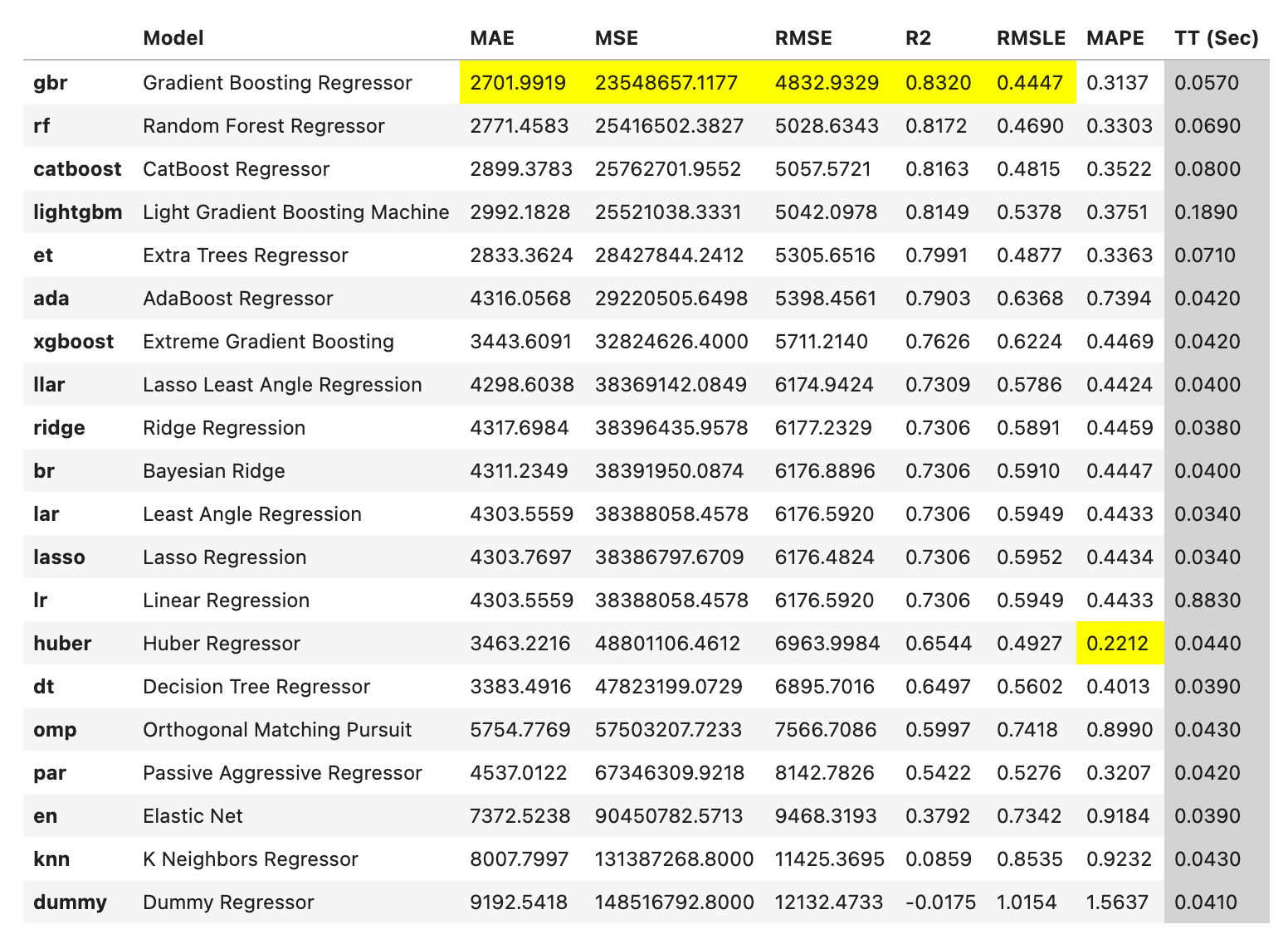
- Gradient Boosting Regressor (gbr):梯度提升回归器是一种集成学习方法,它通过结合多个弱预测模型(通常是决策树)来提高预测的准确性。
- Random Forest Regressor (rf):随机森林是一种集成学习方法,它通过结合多个决策树的预测结果来提高预测的准确性和稳定性。
- CatBoost Regressor (catboost):CatBoost 是一种基于梯度提升的机器学习算法,它特别适合处理分类和回归任务中的类别特征。
- Light Gradient Boosting Machine (lightgbm):LightGBM 是一种基于梯度提升的机器学习算法,它比传统的 GBDT 更快,内存使用更少,准确率更高。
- Extra Trees Regressor (et):Extra Trees 回归器是一种随机森林的变体,它在构建决策树时使用了更多的随机性。
- AdaBoost Regressor (ada):AdaBoost 是一种自适应的提升方法,它通过在每一轮中增加之前预测错误的样本的权重来提高预测的准确性。
- Extreme Gradient Boosting (xgboost):XGBoost 是一种优化的分布式梯度提升库,旨在实现高效,灵活和便携。它在许多机器学习竞赛中都取得了优秀的成绩。
- Lasso Least Angle Regression (llar):Lasso 最小角度回归是一种回归分析方法,它结合了最小角度回归(LAR)和 Lasso 回归的特性。
- Ridge Regression (ridge):Ridge 回归是一种用于处理共线性的线性回归修改版。它通过在损失函数中添加一个正则项(L2 正则化)来防止过拟合。
- Bayesian Ridge (br):贝叶斯岭回归是一种贝叶斯线性回归模型,它使用岭回归的形式,并且参数的选择是通过贝叶斯推断进行的。
- Least Angle Regression (lar):最小角度回归是一种用于高维数据的回归算法,它比传统的步进方法更稳定。
- Lasso Regression (lasso):Lasso 回归是一种回归分析方法,它通过在损失函数中添加一个正则项(L1 正则化)来进行特征选择和防止过拟合。
- Linear Regression (Ir):线性回归是一种基本的预测模型,它假设目标变量和输入特征之间存在线性关系。
- Huber Regressor (huber):Huber 回归是一种鲁棒的回归方法,它结合了线性回归和中位数回归的优点,对于异常值具有较好的鲁棒性。
- Decision Tree Regressor (dt):决策树回归器是一种简单的回归模型,它通过一系列的问题来预测输入样本的值。
- Orthogonal Matching Pursuit (omp):正交匹配追踪是一种贪婪算法,用于近似解决稀疏线性预测模型的问题。
- Passive Aggressive Regressor (par):被动攻击回归是一种在线学习算法,它对预测错误进行更新,但对预测正确的样本保持不变。
- Elastic Net (en):弹性网络是一种线性回归模型,它结合了 Lasso 和 Ridge 的正则化项,可以进行特征选择并防止过拟合。
- K Neighbors Regressor (knn):K 最近邻回归是一种基于实例的学习,它根据输入样本的 k 个最近邻居的平均值或中位数来预测输入样本的值。
- Dummy Regressor (dummy):Dummy 回归器不是真正的回归器,它只是简单地使用规则来预测值,例如,总是预测平均值或中位数。它通常用作基准来比较其他真正的回归器的性能。
聚类


- K-Means Clustering (kmeans):K-均值聚类是一种迭代的聚类算法,它把 n 个观测值分为 k 个聚类,每个聚类的中心是当前所包含成员的均值。
- Affinity Propagation (ap):亲和力传播是一种基于数据点之间的"信息传递"的聚类算法。与 K-均值或 K-中心点等需要预先指定聚类数量的算法不同,亲和力传播自动确定聚类的数量。
- Mean Shift Clustering (meanshift):均值漂移聚类是一种基于密度的聚类算法,它通过更新候选聚类中心来最大化密度函数。
- Spectral Clustering (sc):谱聚类是一种基于图论的聚类方法,它使用数据的谱(即特征向量)信息来进行聚类。
- Agglomerative Clustering (hclust):凝聚层次聚类是一种层次聚类方法,它开始时每个观测值各自为一个聚类,然后合并最近的一对聚类,如此重复直到所有的观测值都在一个聚类中。
- Density-Based Spatial Clustering (dbscan):DBSCAN 是一种基于密度的聚类算法,它将密度高且相连的区域划分为同一聚类。
- OPTICS Clustering (optics):OPTICS(Ordering Points To Identify the Clustering Structure)是一种改进的基于密度的聚类方法,它可以找到在密度上有显著差异的空间聚类。
- Birch Clustering (birch):BIRCH(Balanced Iterative Reducing and Clustering using Hierarchies)是一种用于大数据集的聚类方法,它通过构建一个聚类特征树来减少数据的复杂性。
- K-Modes Clustering (kmodes):K-模式聚类是 K-均值聚类的一种变体,它用于分类数据。与 K-均值不同,K-模式使用模式(最常见的值)而不是均值来定义聚类中心。
异常检测
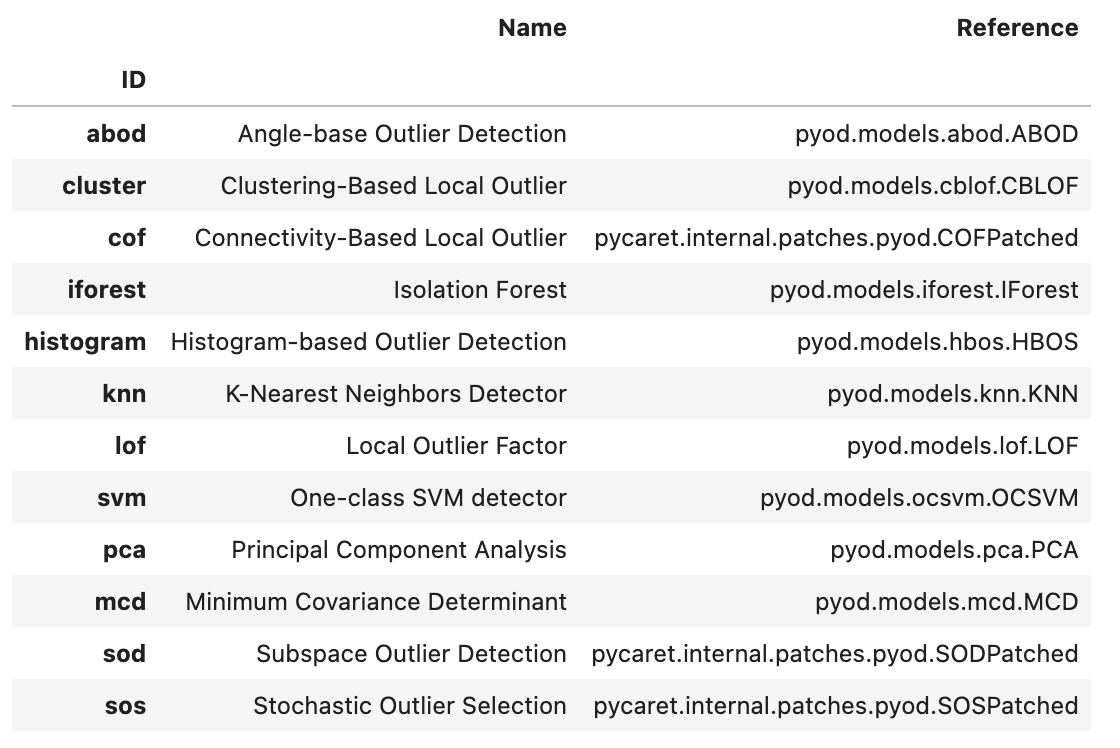
- Angle-base Outlier Detection (abod):基于角度的异常检测是一种多元数据的异常检测方法,它考虑了数据点之间的角度信息。
- Clustering-Based Local Outlier (cluster):基于聚类的局部异常检测是一种异常检测方法,它首先进行聚类,然后根据数据点到其所在聚类中心的距离来判断其是否为异常。
- Connectivity-Based Local Outlier (cof):基于连接的局部异常因子是一种异常检测方法,它考虑了数据点的邻居之间的连接性。
- Isolation Forest (iforest):孤立森林是一种高效的异常检测算法,它通过随机选择特征并随机选择这些特征的分割值来孤立观测值。
- Histogram-based Outlier Detection (histogram):基于直方图的异常检测是一种无监督的异常检测方法,它通过构建数据的直方图来检测异常。
- K-Nearest Neighbors Detector (knn):K-最近邻检测器是一种异常检测方法,它根据数据点到其 k 个最近邻居的距离来判断其是否为异常。
- Local Outlier Factor (lof):局部异常因子是一种基于密度的异常检测方法,它考虑了数据点的局部密度和其邻居的局部密度。
- One-class SVM detector (svm):单类 SVM 是一种无监督的异常检测方法,它试图找到一个决策边界来分隔正常数据和异常数据。
- Principal Component Analysis (pca):主成分分析是一种降维方法,它可以用于异常检测,通过将数据投影到由主成分构成的低维空间,然后根据重构误差来检测异常。
- Minimum Covariance Determinant (mcd):最小协方差行列式是一种鲁棒的多元异常检测方法,它假设正常数据遵循多元高斯分布,但是协方差矩阵是由异常值鲁棒估计的。
- Subspace Outlier Detection (sod):子空间异常检测是一种基于子空间的异常检测方法,它考虑了数据的高维和子空间结构。
- Stochastic Outlier Selection (sos):随机异常选择是一种基于概率的异常检测方法,它为每个数据点分配一个异常得分,这个得分表示其他数据点将其视为异常的概率。
时间序列
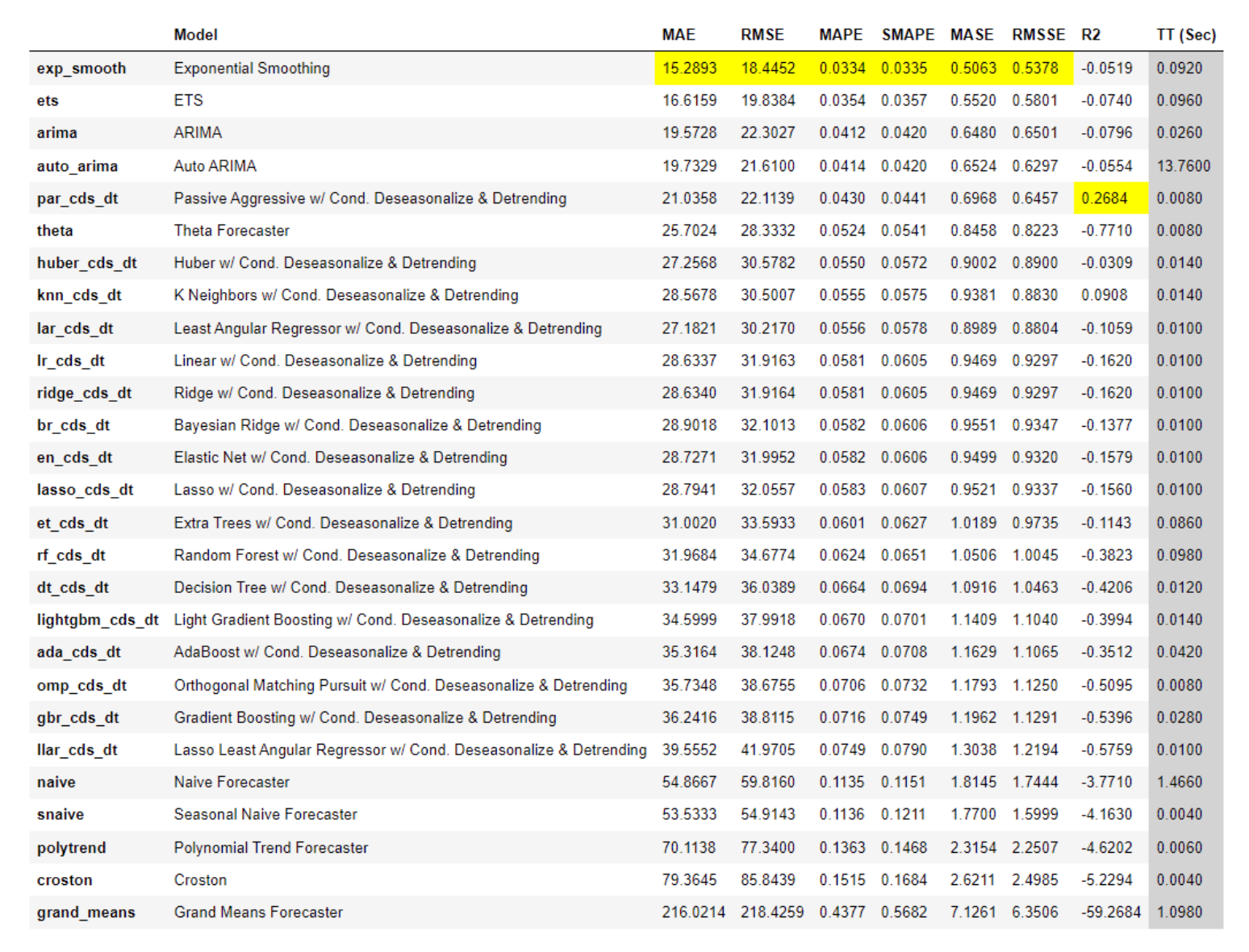
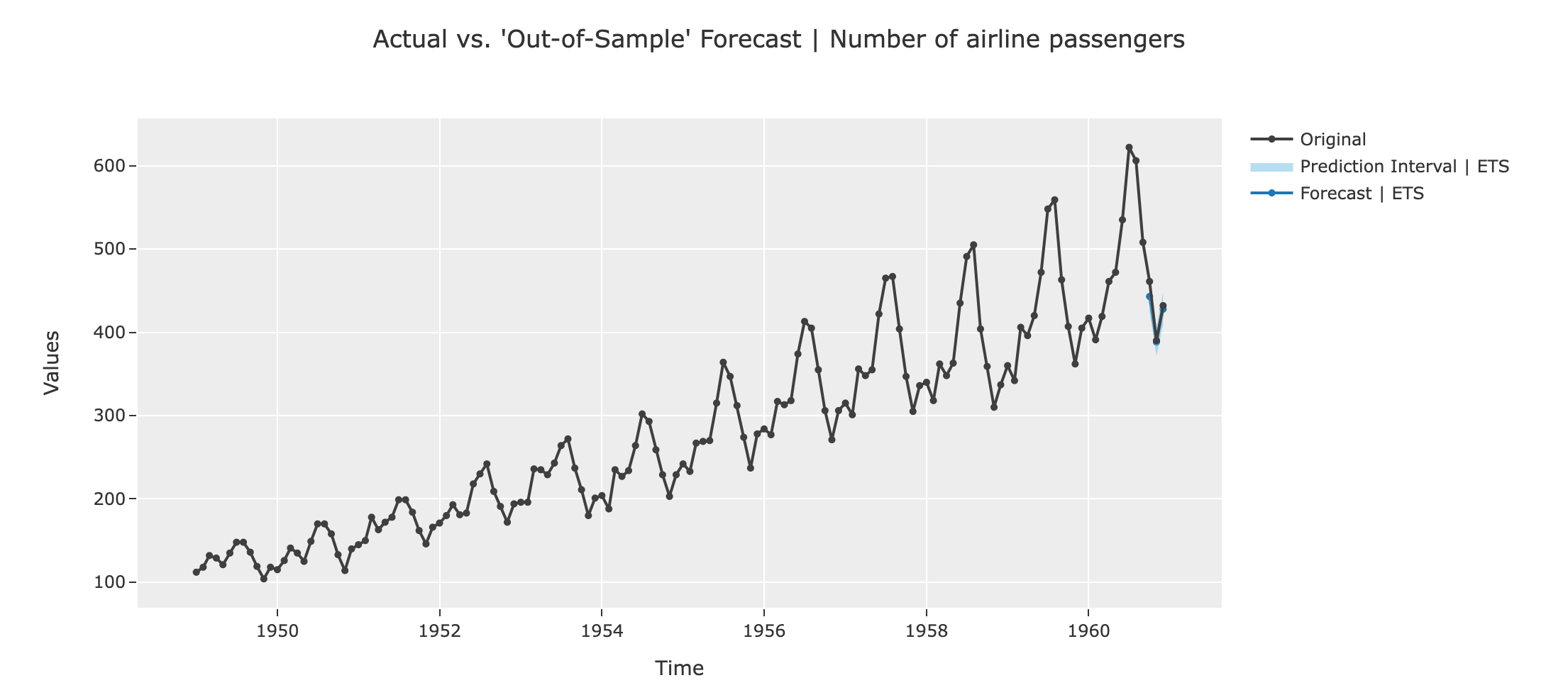
- ETS (ets):ETS(Error, Trend, Seasonality)模型是一种常用的时间序列预测模型,它包括误差、趋势和季节性三个组成部分。
- Exponential Smoothing (exp_smooth):指数平滑是一种时间序列预测方法,它使用过去观测值的加权平均作为未来的预测。
- ARIMA (arima):ARIMA(自回归整合移动平均)模型是一种常用的时间序列预测模型,它包括自回归、差分和移动平均三个部分。
- Auto ARIMA (auto_arima):自动 ARIMA 是一种自动选择最优 ARIMA 参数的方法。
- Passive Aggressive w/Cond.Deseasonalize Detrending (par_cds_dt):这是一种结合了被动攻击回归和条件去季节性趋势的预测方法。
- Least Angular Regressor w/Cond.Deseasonalize Detrending (lar_cds_dt):这是一种结合了最小角度回归和条件去季节性趋势的预测方法。
- Huber w/Cond.Deseasonalize Detrending (huber_cds_dt):这是一种结合了 Huber 回归和条件去季节性趋势的预测方法。
- Linear w/Cond.Deseasonalize Detrending (Ir_cds_dt):这是一种结合了线性回归和条件去季节性趋势的预测方法。
- Ridge w/Cond.Deseasonalize Detrending (ridge_cds_dt):这是一种结合了岭回归和条件去季节性趋势的预测方法。
- Elastic Net w/Cond.Deseasonalize Detrending (en_cds_dt):这是一种结合了弹性网络回归和条件去季节性趋势的预测方法。
- Lasso w/Cond.Deseasonalize Detrending (lasso_cds_dt):这是一种结合了 Lasso 回归和条件去季节性趋势的预测方法。
- Bayesian Ridge w/Cond.Deseasonalize Detrending (br_cds _dt):这是一种结合了贝叶斯岭回归和条件去季节性趋势的预测方法。
- K Neighbors w/Cond.Deseasonalize Detrending (knn_cds_dt):这是一种结合了 K 最近邻回归和条件去季节性趋势的预测方法。
- Theta Forecaster (theta):Theta 预测器是一种简单的时间序列预测方法,它基于对时间序列进行线性变换。
- Extra Trees w/Cond.Deseasonalize Detrending (et_cds_dt):这是一种结合了 Extra Trees 回归和条件去季节性趋势的预测方法。
- Decision Tree w/Cond.Deseasonalize Detrending (dt_cds_dt):这是一种结合了决策树回归和条件去季节性趋势的预测方法。
- Light Gradient Boosting w/Cond.Deseasonalize Detrending (lightgbm_cds_dt):这是一种结合了 LightGBM 和条件去季节性趋势的预测方法。
- Orthogonal Matching Pursuit w/Cond.Deseasonalize Detrending (omp_cds_dt):这是一种结合了正交匹配追踪和条件去季节性趋势的预测方法。
- Gradient Boosting w/Cond.Deseasonalize Detrending (gbr_cds_dt):这是一种结合了梯度提升回归和条件去季节性趋势的预测方法。
- Random Forest w/Cond.Deseasonalize Detrending (rf_cds_dt):这是一种结合了随机森林回归和条件去季节性趋势的预测方法。
- CatBoost Regressor w/Cond.Deseasonalize Detrending (catboost_cds_dt):这是一种结合了 CatBoost 回归和条件去季节性趋势的预测方法。
- AdaBoost w/Cond.Deseasonalize Detrending (ada_cds_dt):这是一种结合了 AdaBoost 回归和条件去季节性趋势的预测方法。
- Extreme Gradient Boosting w/Cond.Deseasonalize Detrending (xgboost_cds_dt):这是一种结合了 XGBoost 和条件去季节性趋势的预测方法。
- Lasso Least Angular Regressor w/Cond.Deseasonalize Detrending (llar_cds_dt):这是一种结合了 Lasso 最小角度回归和条件去季节性趋势的预测方法。
- Naive Forecaster (naive):朴素预测器是一种简单的时间序列预测方法,它假设未来的值等于最近的观测值。
- Seasonal Naive Forecaster (snaive):季节性朴素预测器是一种简单的时间序列预测方法,它假设未来的值等于上一季度的值。
- Polynomial Trend Forecaster (polytrend):多项式趋势预测器是一种时间序列预测方法,它假设时间序列的趋势可以用多项式来描述。
- Croston (croston):Croston 方法是一种用于预测稀疏需求时间序列的方法。
- Grand Means Forecaster (grand_means):大平均预测器是一种简单的时间序列预测方法,它假设未来的值等于所有历史观测值的平均值。
模型调优
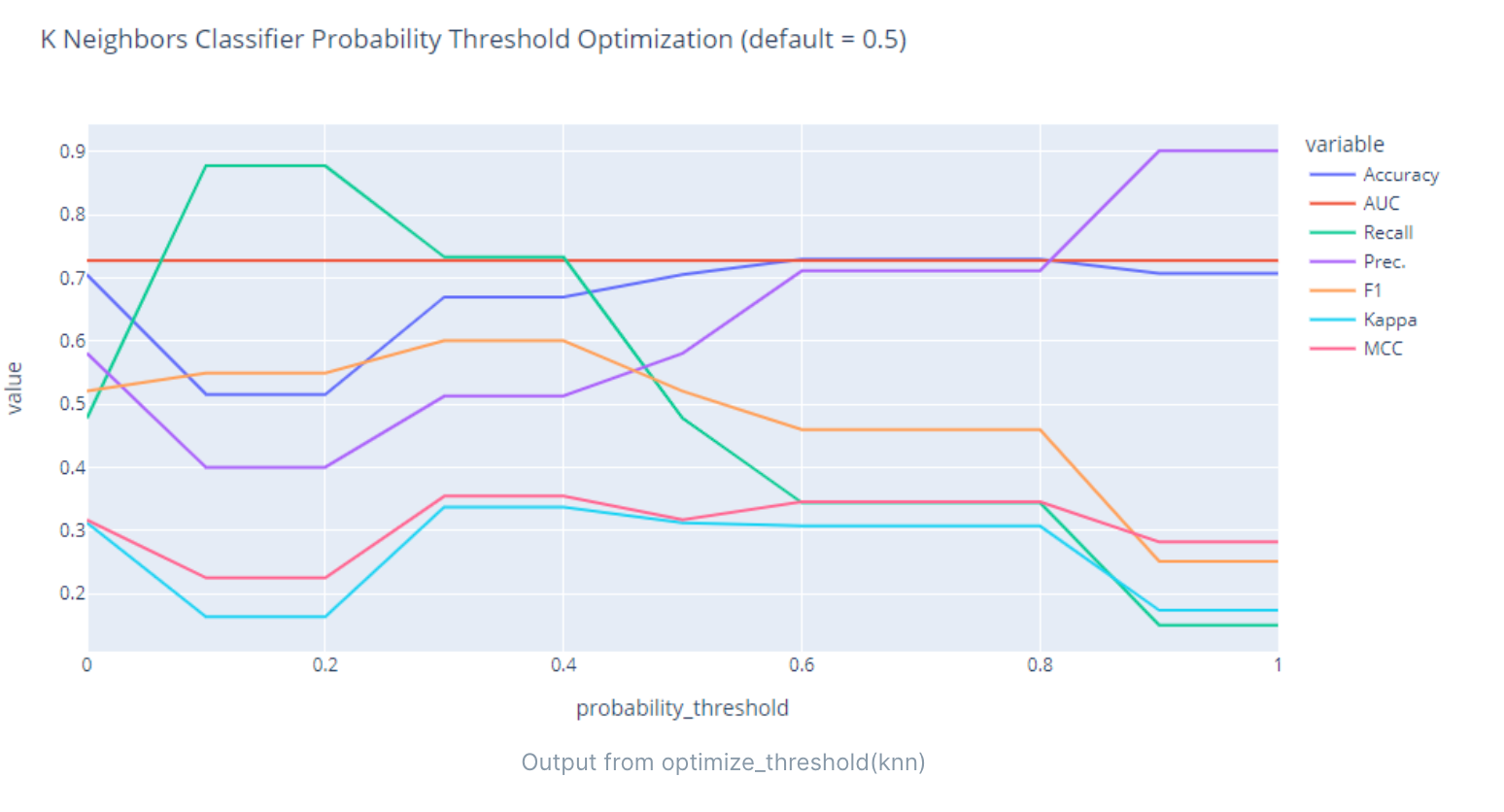
- 选择正确的评估指标或自定义评估指标(如auc最优、recall最优等)
- 网格搜索调优
校准模型
在机器学习中,分类模型不仅可以预测样本的类别,还可以预测样本属于某个类别的概率。然而,模型预测的概率可能并不准确,即模型预测的概率与真实的概率不一致。这就需要对模型的预测概率进行校准。
概率校准的目的是使模型预测的概率更接近真实的概率。例如,如果模型预测一个样本属于正类的概率为0.8,我们希望在所有模型预测概率为0.8的样本中,大约有80%的样本是正类。
需要注意的是,虽然概率校准可以提高模型预测概率的准确性,但它可能会降低模型在其他评价指标(如准确率、AUC等)上的表现。因此,是否需要进行概率校准以及选择何种校准方法,需要根据具体的应用场景和评价标准来决定。
概率校准的基本思想是对模型的原始预测概率进行一定的调整,使其更接近真实的概率。这通常通过学习一个映射函数来实现,该函数将模型的原始预测概率映射到校准后的概率。
举个例子来看看,假设我们有一个二分类问题,模型的原始预测概率如下:
- 样本1:0.8
- 样本2:0.7
- 样本3:0.6
- 样本4:0.8
- 样本5:0.7
然后,我们查看这些样本的真实类别,发现样本1和样本4是正类,其他样本是负类。也就是说,当模型预测概率为0.8时,真实的正类概率是0.5(1/2),而不是0.8。同样,当模型预测概率为0.7时,真实的正类概率是0(0/2),而不是0.7。
于是,我们可以学习一个映射函数,将模型的原始预测概率映射到校准后的概率。例如,我们可以设定当原始预测概率为0.8时,校准后的预测概率为0.5;当原始预测概率为0.7时,校准后的预测概率为0。
这样,我们就可以用校准后的预测概率替代原始预测概率,使模型的预测概率更接近真实的概率。这个例子是很简化的,实际中校准通常会基于训练数据集进行,并且映射函数可能是线性的(如Platt校准)或者非线性的(如Isotonic校准)。
需要注意的是,概率校准不会改变模型的预测类别,只会改变模型的预测概率。如果你只关心模型的预测类别,而不关心预测概率,那么可能不需要进行概率校准。
模型评估
分类
- Accuracy:准确率是分类正确的样本数占总样本数的比例。它是最直观的分类性能指标,但在类别不平衡的情况下可能会产生误导。
- AUC (Area Under the Curve):AUC 是 ROC 曲线下的面积。ROC 曲线是以假阳性率(FPR)为横轴,真阳性率(TPR)为纵轴绘制的曲线。AUC 的值介于 0.5 和 1 之间,值越大表示分类性能越好。
- Recall:召回率(也称为真阳性率)是真实为正类的样本中被正确预测为正类的比例。它衡量了模型找出正类样本的能力。
- Precision:精确率是预测为正类的样本中真实为正类的比例。它衡量了模型预测正类的准确性。
- F1:F1 分数是精确率和召回率的调和平均值,它试图在这两个指标之间找到一个平衡。
- Kappa:Kappa 系数是一种考虑了随机预测的准确率的指标。它的值介于 -1 和 1 之间,值越大表示分类性能越好。
- MCC (Matthews Correlation Coefficient):Matthews 相关系数是一种在类别不平衡的情况下评估二元分类性能的指标。它的值介于 -1 和 1 之间,值越大表示分类性能越好。
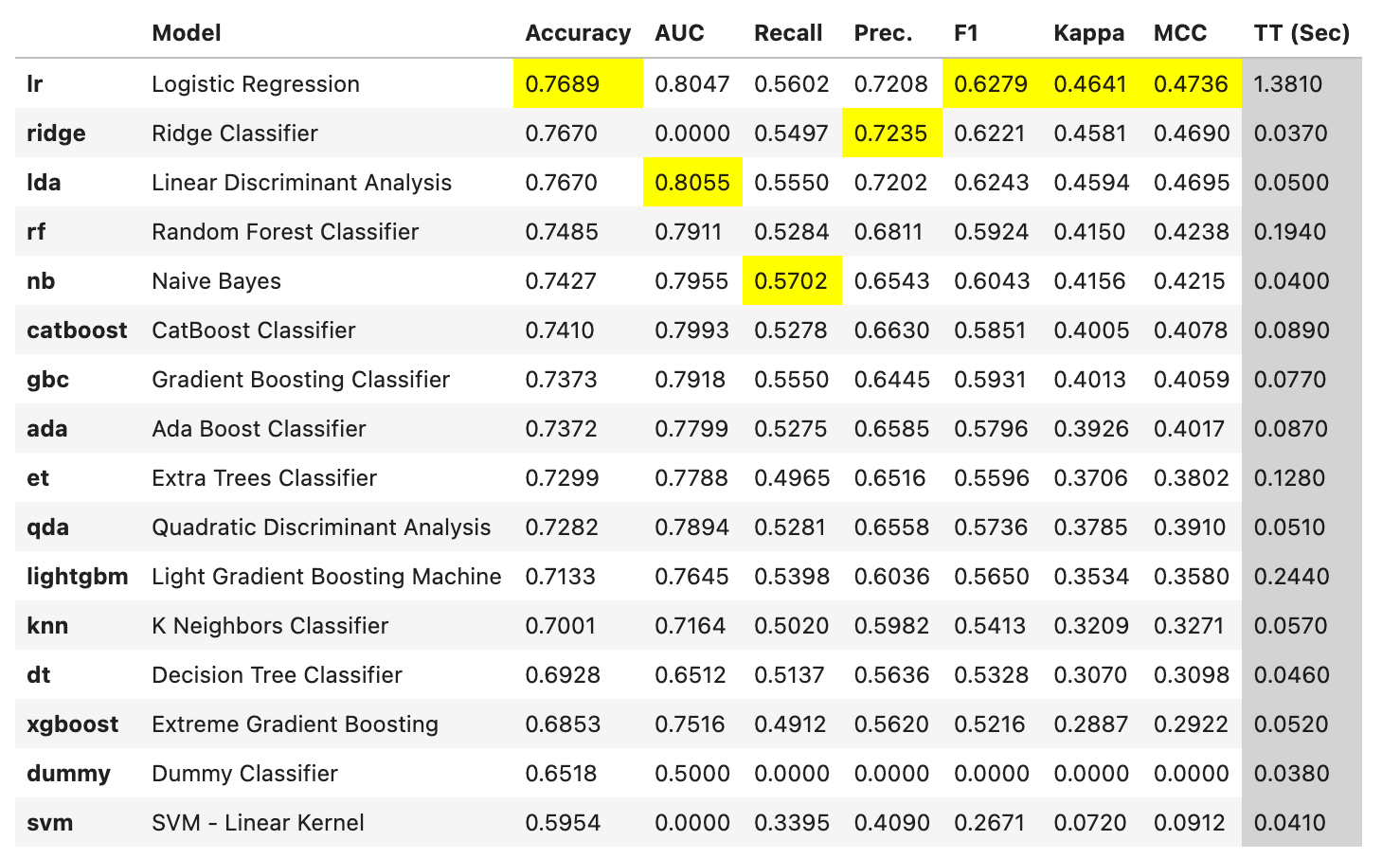
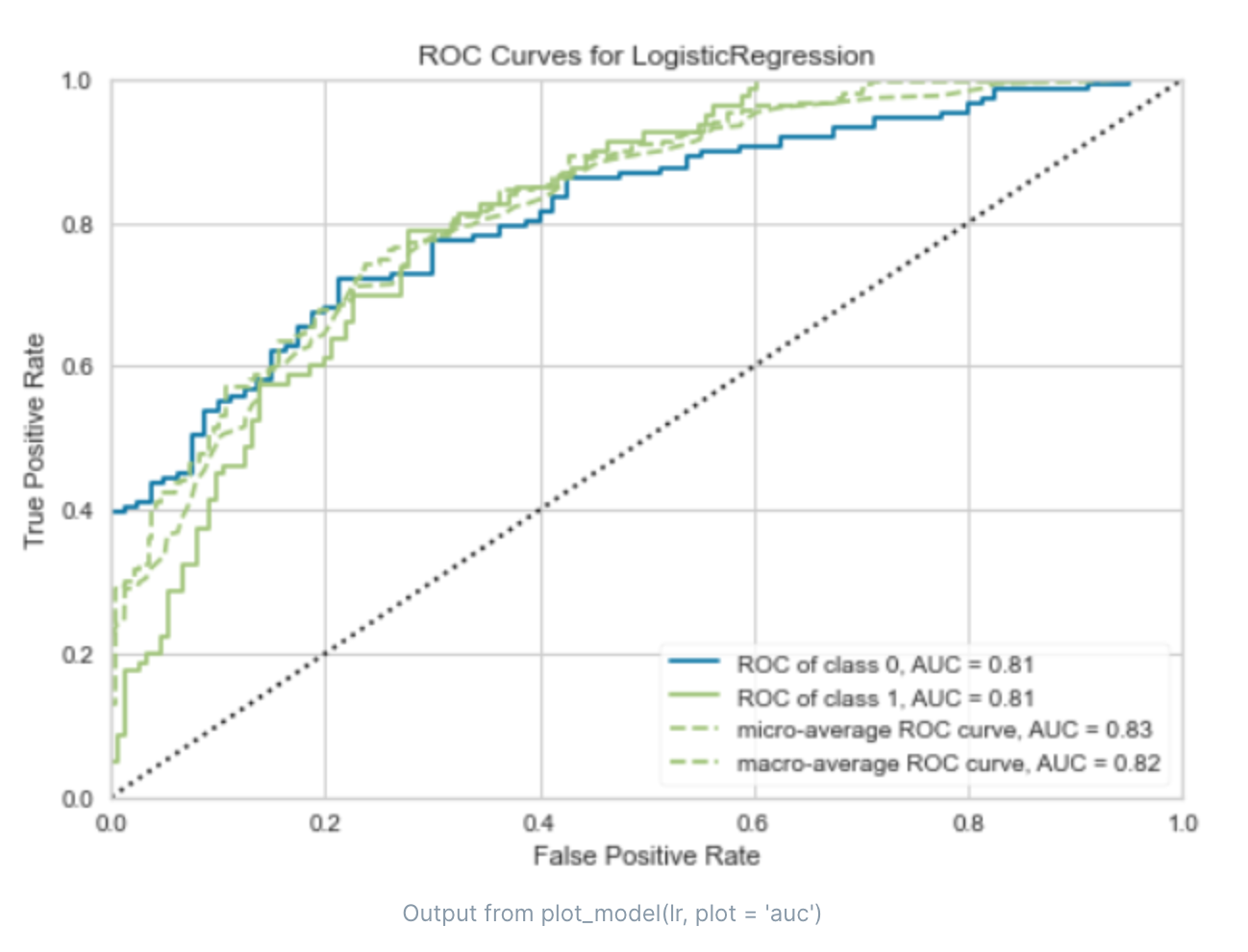
ROC曲线(Receiver Operating Characteristic curve)是一种用于评估二元分类器性能的图形工具。ROC曲线的横轴是“假阳性率”(False Positive Rate,FPR),纵轴是“真阳性率”(True Positive Rate,TPR)。
真阳性率(TPR)也被称为召回率,是真实为正类的样本中被正确预测为正类的比例。它衡量了分类器找出正类样本的能力。
假阳性率(FPR)是真实为负类的样本中被错误预测为正类的比例。它衡量了分类器在预测负类样本时犯错误的频率。
ROC曲线是通过改变分类阈值来绘制的。当阈值变化时,TPR和FPR也会随之变化,从而得到一系列的点,连接这些点就得到了ROC曲线。
ROC曲线的特点是:
ROC曲线越接近左上角,分类器的性能越好。理想的情况是TPR=1,FPR=0,即所有的正样本都被正确分类,没有负样本被错误分类,此时ROC曲线会经过左上角。
ROC曲线下的面积(AUC,Area Under Curve)可以用来量化分类器的整体性能。AUC的值介于0.5(等同于随机猜测)和1(完美分类器)之间。
ROC曲线对于类别不平衡问题相对鲁棒,即使在正负样本比例变化的情况下,ROC曲线的形状和AUC值通常不会发生大的变化。
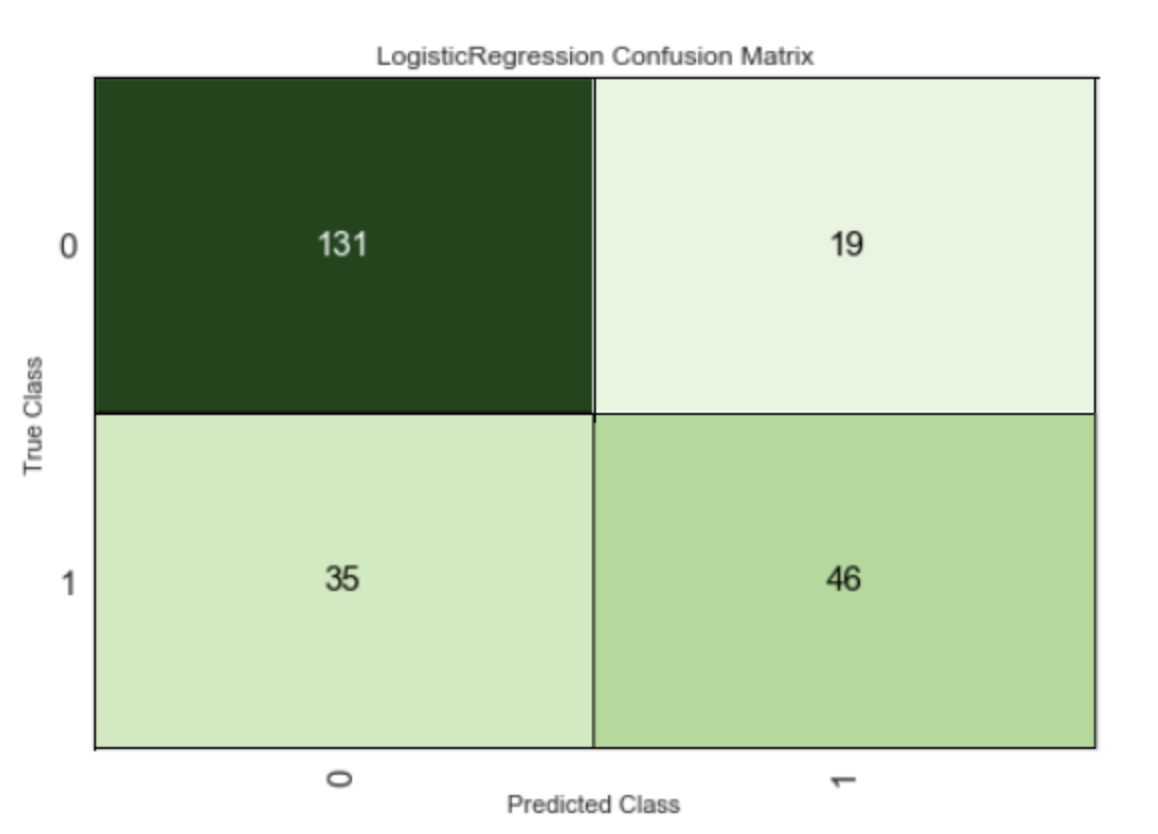
混淆矩阵(Confusion Matrix)是一种特定的表格布局,用于可视化监督学习算法的性能,特别是在二元或多类分类问题中。在混淆矩阵中,每一行代表实际的类别,每一列代表预测的类别。对于二元分类问题,混淆矩阵通常如下:
预测为正类 预测为负类 实际为正类 真阳性(TP) 假阴性(FN) 实际为负类 假阳性(FP) 真阴性(TN)各项的含义如下:
- 真阳性(True Positive, TP):实际为正类且预测为正类的样本数。
- 假阴性(False Negative, FN):实际为正类但预测为负类的样本数。
- 假阳性(False Positive, FP):实际为负类但预测为正类的样本数。
- 真阴性(True Negative, TN):实际为负类且预测为负类的样本数。
混淆矩阵可以帮助我们理解分类器的性能,特别是它的错误类型。例如,假阳性和假阴性通常有不同的实际成本。此外,许多常用的分类性能指标,如准确率、精确率、召回率和 F1 分数,都可以从混淆矩阵中计算得出。
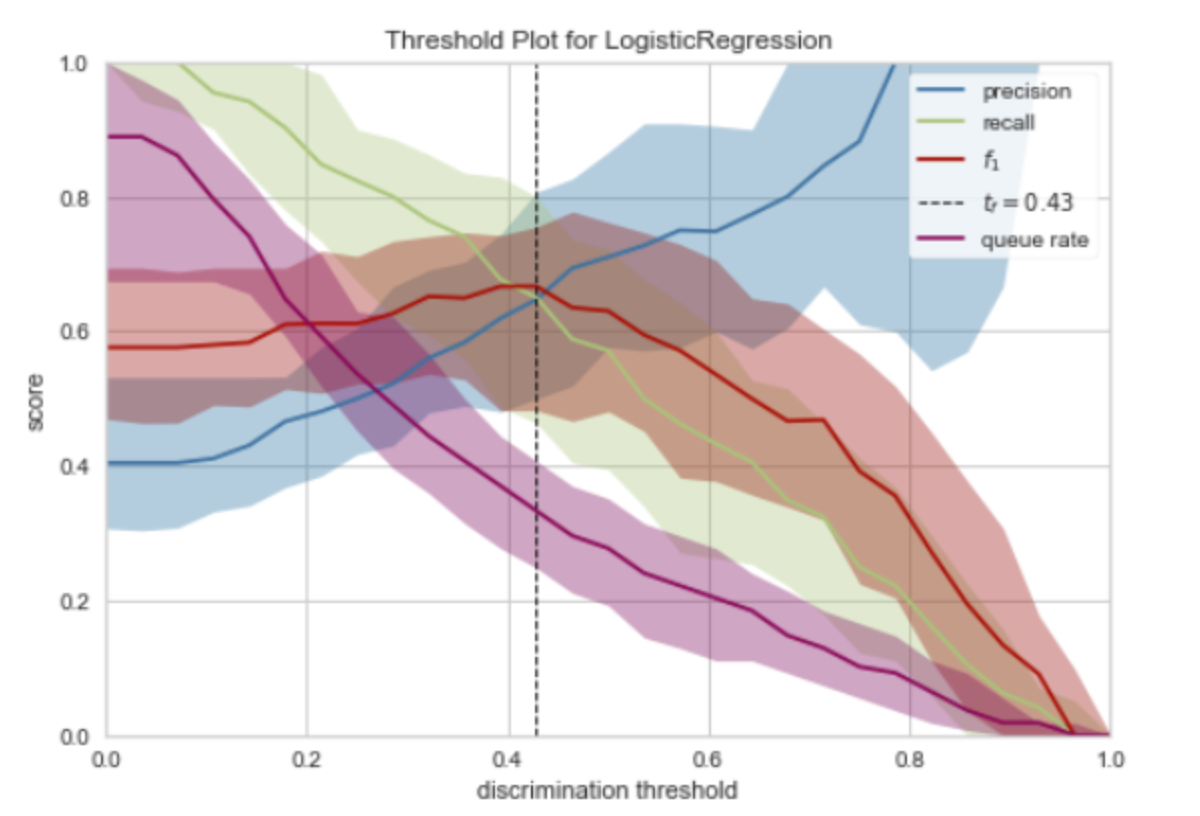
- 各指标随着阈值变化的情况
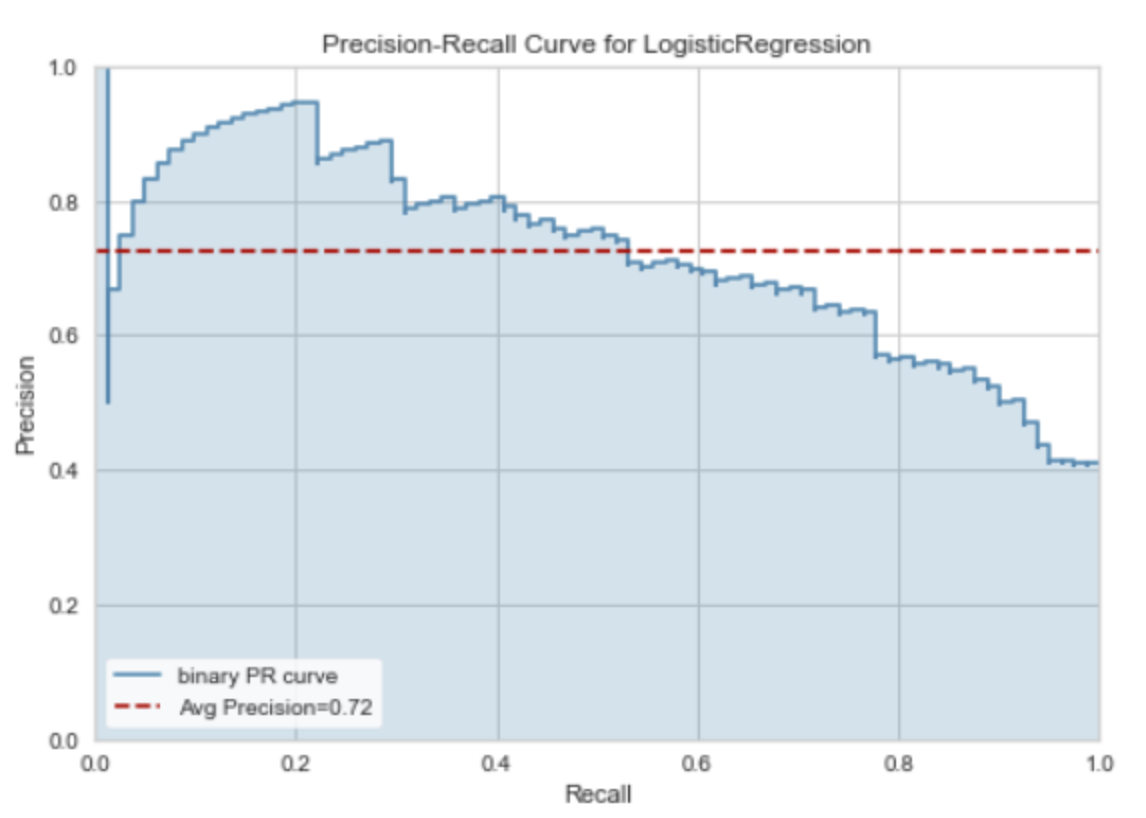
PR曲线(Precision-Recall Curve)是一种用于评估二元分类器性能的图形工具,特别是在正负样本不平衡的情况下。PR曲线的横轴是“召回率”(Recall),纵轴是“精确率”(Precision)。
- 精确率(Precision)是预测为正类的样本中真实为正类的比例。它衡量了分类器预测正类的准确性。
- 召回率(Recall)也被称为真阳性率,是真实为正类的样本中被正确预测为正类的比例。它衡量了分类器找出正类样本的能力。
PR曲线是通过改变分类阈值来绘制的。当阈值变化时,Precision和Recall也会随之变化,从而得到一系列的点,连接这些点就得到了PR曲线。
PR曲线的特点是:
- PR曲线越接近右上角,分类器的性能越好。理想的情况是Precision=1,Recall=1,即所有的正样本都被正确分类,没有负样本被错误分类,此时PR曲线会经过右上角。
- PR曲线下的面积(AUC-PR,Area Under the PR Curve)可以用来量化分类器的整体性能。AUC-PR的值介于0(最差)和1(最好)之间。
- PR曲线对于类别不平衡问题非常敏感,即使在正负样本比例变化的情况下,PR曲线的形状和AUC-PR值通常会发生大的变化。因此,当正负样本比例严重不平衡时,PR曲线通常比ROC曲线更能反映分类器的真实性能。
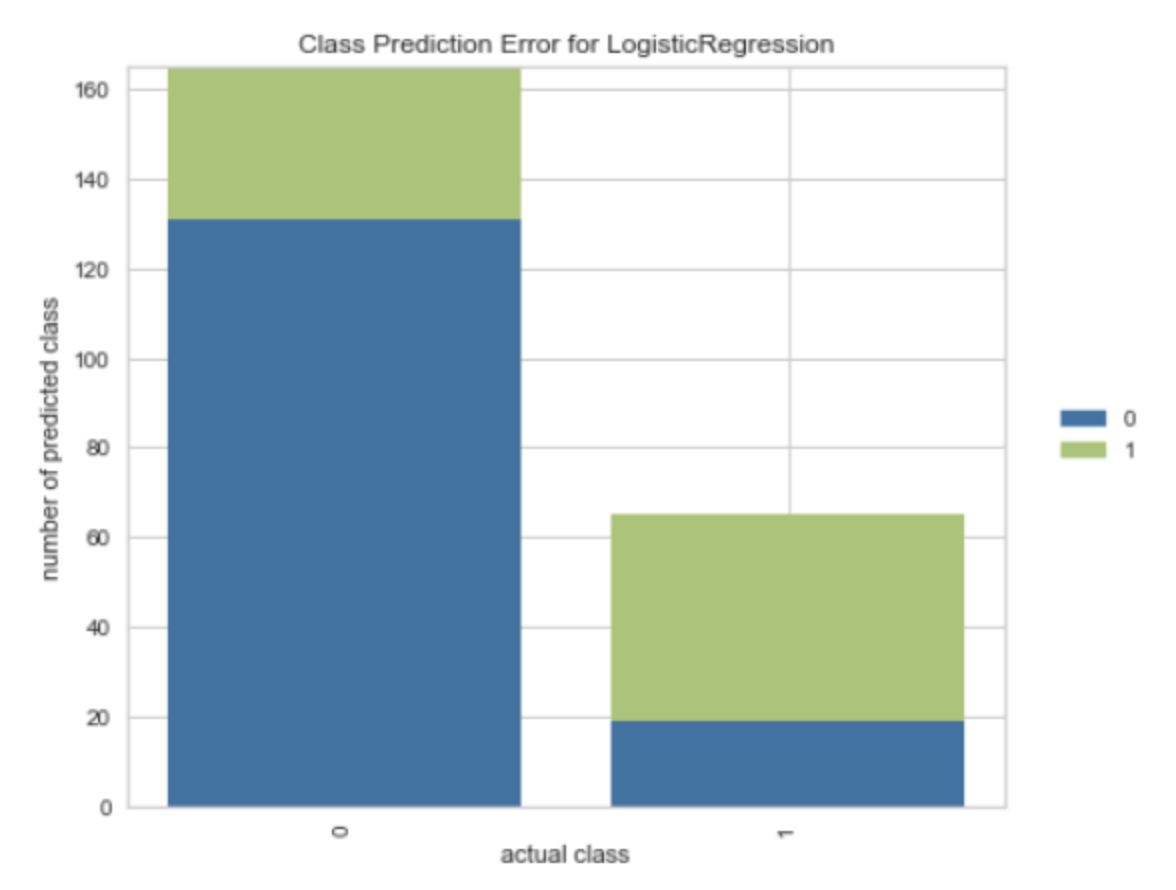
- 各真实类别的预测准确率
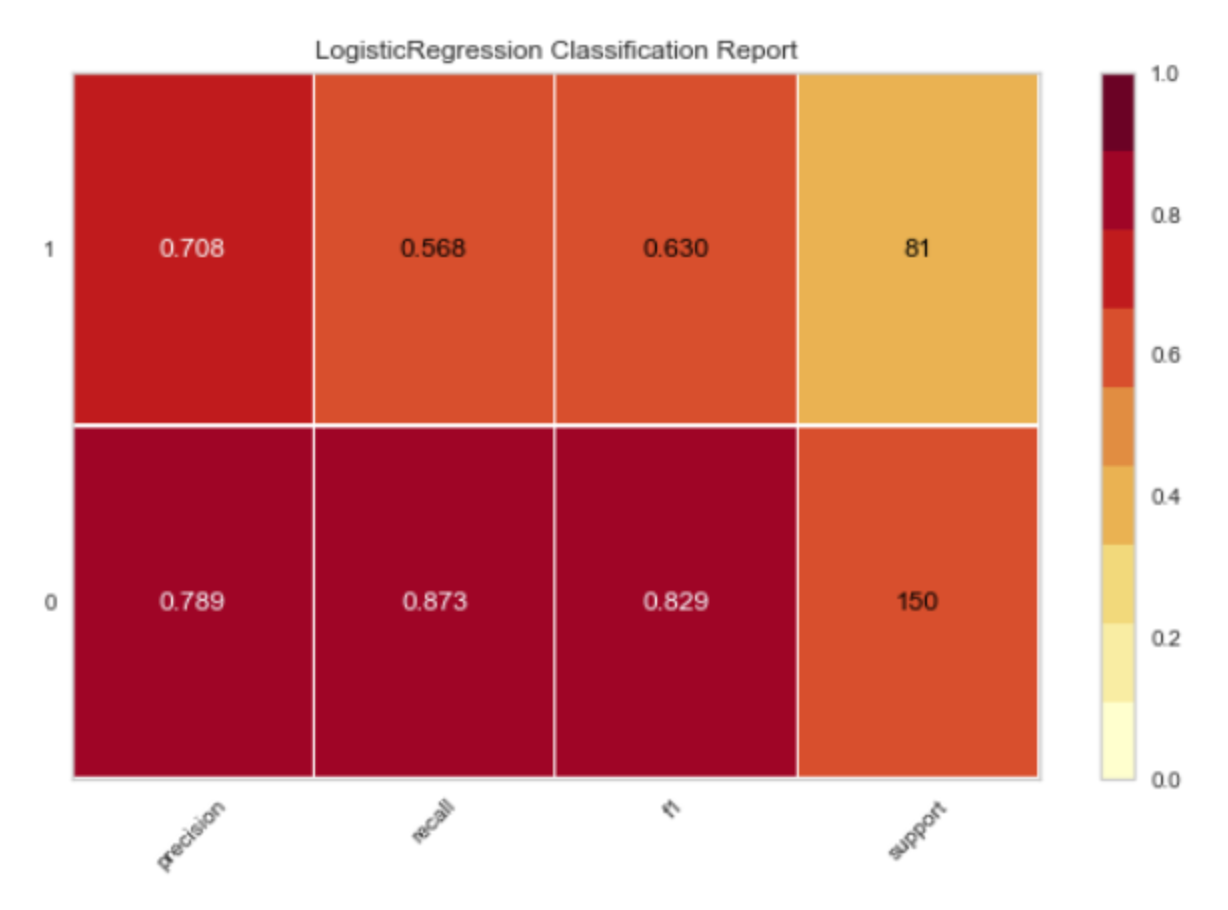
- 分类报告
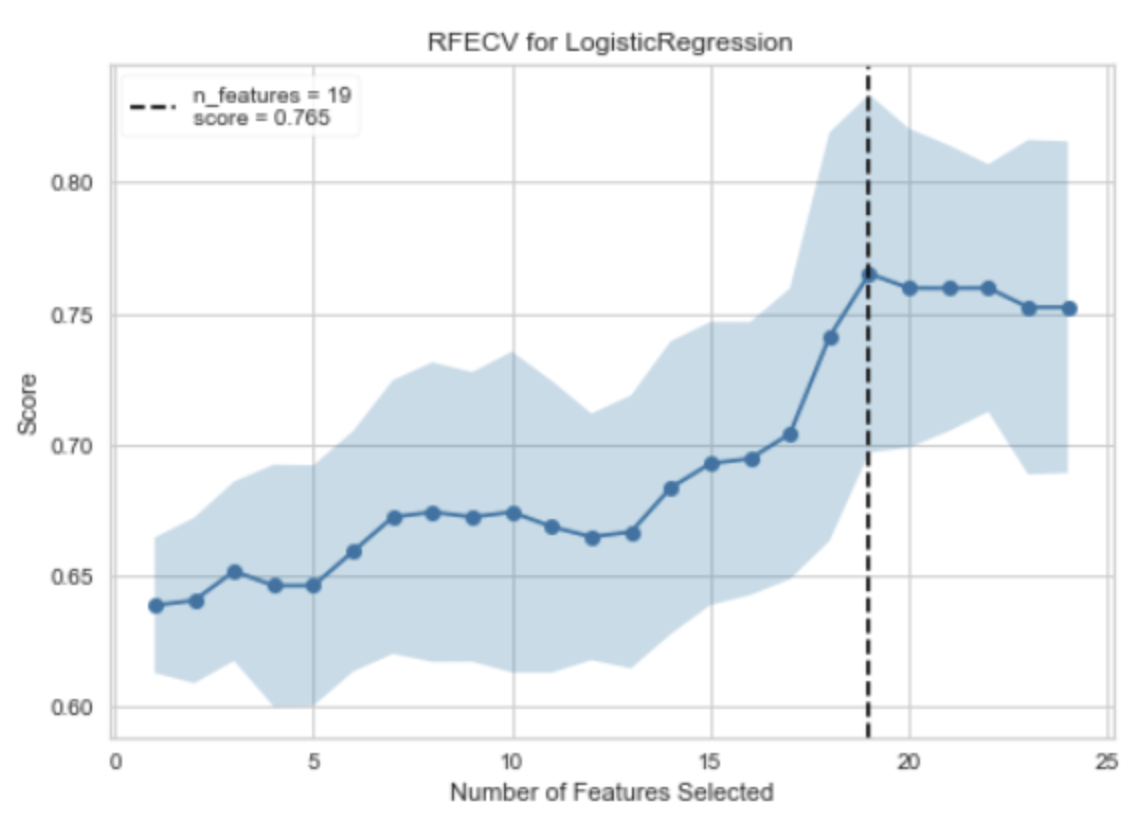
RFECV是 Recursive Feature Elimination with Cross-Validation(带交叉验证的递归特征消除)的缩写,它是一种特征选择方法,用于自动找出对模型预测最有贡献的特征。RFECV的工作原理是反复构建模型,然后选择出最好的(或最差的)特征(可以通过coef_属性或者feature_importances_属性来获取),把选出的特征放置一边,然后在剩余的特征上重复该过程,直到所有特征都遍历完。这个过程中使用的模型需要是能够提供重要性权重或系数的模型,如线性模型,SVM,决策树等。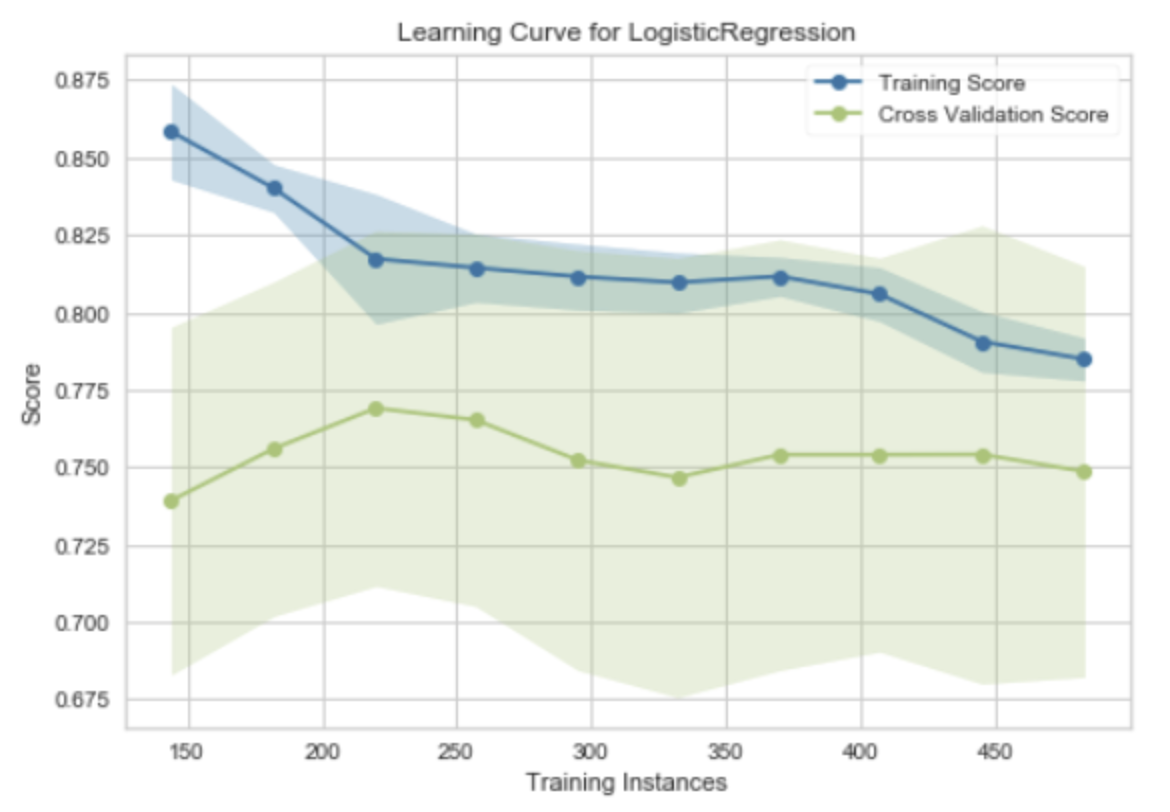
"Learning Curve for Logistic Regression" 是一种用于评估逻辑回归模型性能的工具。学习曲线(Learning Curve)是一种图形,它展示了模型在训练集和验证集(或测试集)上的性能随着训练样本数量的增加而变化的情况。
在学习曲线中,横轴通常是训练样本的数量,纵轴是模型的性能度量,如准确率、损失函数的值等。对于逻辑回归模型,学习曲线可以帮助我们理解更多的训练数据是否能够提高模型的性能。
学习曲线有两条线,一条表示训练误差,另一条表示验证误差:
- 训练误差:这是模型在训练数据上的误差。随着训练样本数量的增加,训练误差通常会增加,因为模型需要拟合更多的数据。
- 验证误差:这是模型在验证数据上的误差。随着训练样本数量的增加,验证误差通常会减少,因为模型得到了更多的信息来学习数据的模式。
通过观察学习曲线,我们可以得到一些关于模型性能的见解,例如,如果训练误差和验证误差之间的差距很大,可能说明模型过拟合;如果两者都很高,可能说明模型欠拟合。
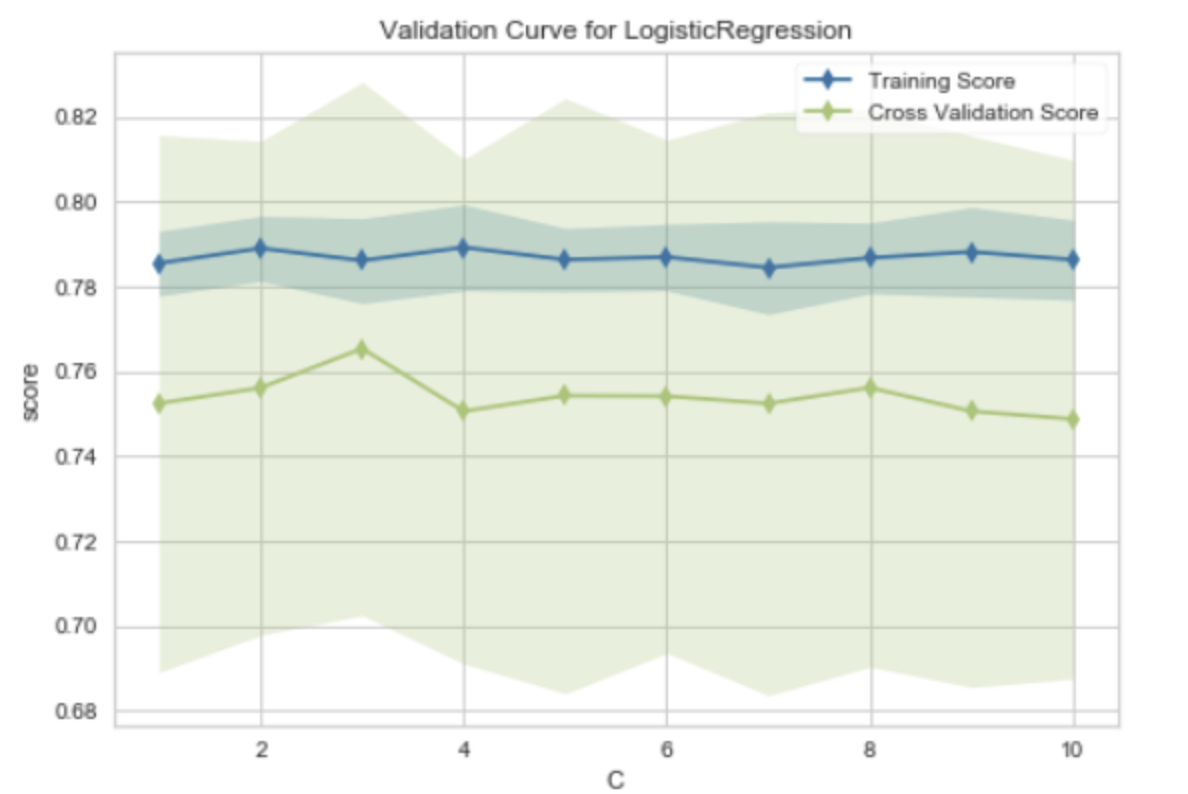
"Validation Curve for Logistic Regression" 是一种用于评估逻辑回归模型性能的工具。验证曲线(Validation Curve)是一种图形,它展示了模型在训练集和验证集(或测试集)上的性能随着模型参数的变化而变化的情况。
在验证曲线中,横轴通常是某个模型参数的值,纵轴是模型的性能度量,如准确率、损失函数的值等。对于逻辑回归模型,验证曲线可以帮助我们理解不同的参数值如何影响模型的性能。
验证曲线有两条线,一条表示训练得分,另一条表示验证得分:
- 训练得分:这是模型在训练数据上的得分。随着模型复杂度的增加(例如,参数值的增加),训练得分通常会增加,因为模型能够更好地拟合训练数据。
- 验证得分:这是模型在验证数据上的得分。随着模型复杂度的增加,验证得分通常先增加后减少。这是因为当模型过于复杂时,它可能会过拟合训练数据,导致在未见过的验证数据上的性能下降。
通过观察验证曲线,我们可以找到模型性能最好的参数值,也可以了解模型是否过拟合或欠拟合。
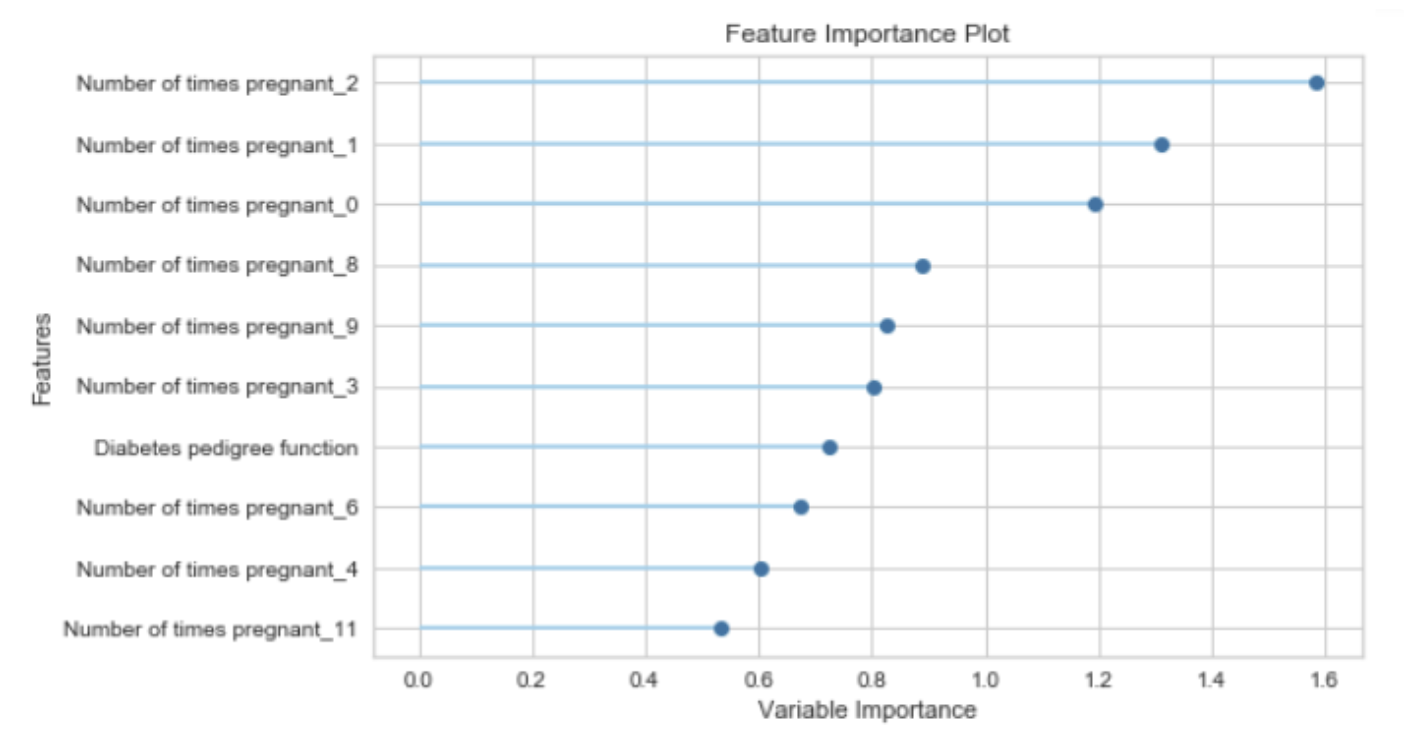
特征重要度(Feature Importance)是一种用于解释机器学习模型的技术,它为输入特征分配一个分数,以表示每个特征对模型预测的贡献大小。特征重要度可以帮助我们理解哪些特征对模型的预测最有影响,从而提供模型的可解释性。
特征重要度的计算方法取决于具体的模型类型。例如:
- 对于决策树模型,特征重要度通常是根据特征在树中的分裂点出现的频率和深度来计算的。一个特征如果在树的顶部(深度较小)并且在多个树中频繁出现,那么它通常被认为是重要的。
- 对于线性模型,特征的系数可以被视为特征重要度。系数的绝对值越大,特征越重要。
- 对于基于梯度提升的模型(如 XGBoost 或 LightGBM),特征重要度可以是基于特征分裂增益的总和,或者是特征被选为分裂点的次数。
值得注意的是,特征重要度只能提供特征和目标变量之间的关系的相对度量,并不能提供特征和目标之间的确切关系(例如,它不能告诉你改变一个特征的值会如何精确地改变预测结果)。此外,特征重要度也不能很好地处理相关特征。如果两个特征高度相关,那么它们的重要度可能会被模型任意分配。
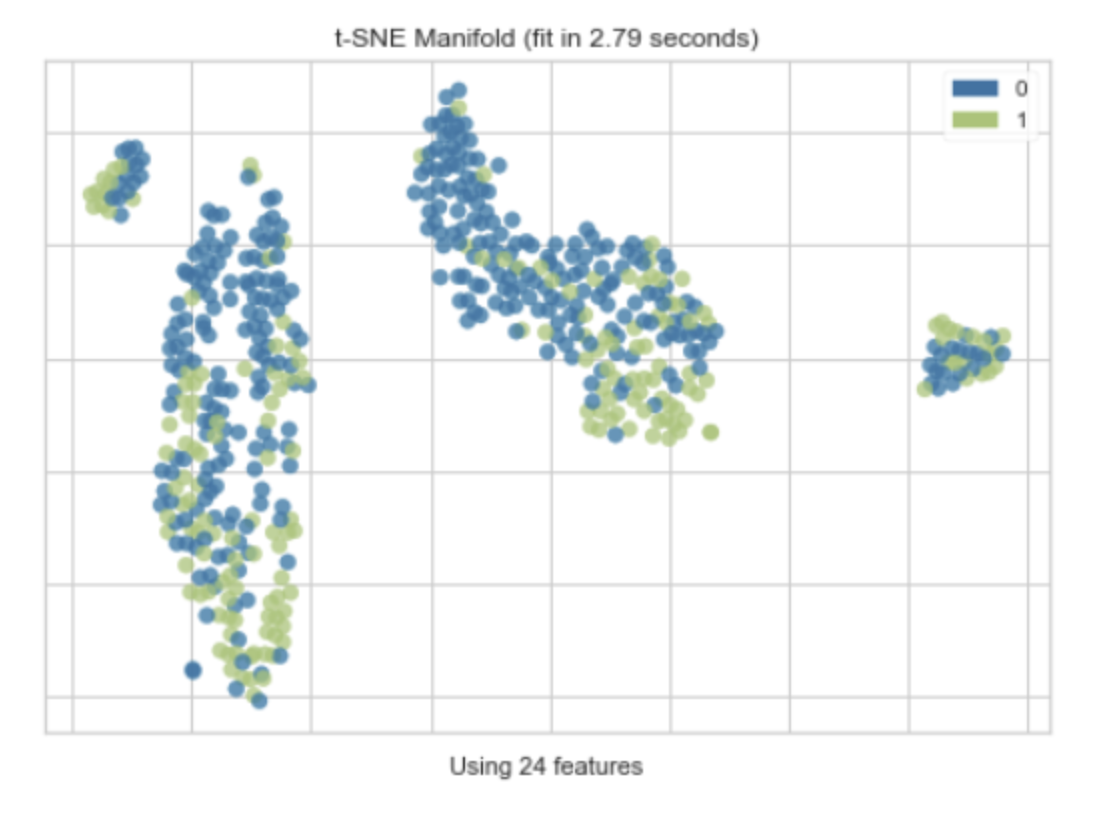
t-SNE(t-Distributed Stochastic Neighbor Embedding)是一种用于数据可视化的工具,特别适用于高维数据的降维和可视化。它是一种非线性的降维方法,可以保持原始高维数据中的局部结构。
t-SNE的工作原理是在高维空间和低维空间(通常是2D或3D,以便于可视化)中都定义一个概率分布,使得相似的对象有更高的概率被选择为邻居。然后,t-SNE优化这两个概率分布的KL散度(Kullback-Leibler divergence),使得低维空间中的概率分布尽可能接近高维空间中的概率分布。
"t-SNE Manifold"通常指的是使用t-SNE方法得到的低维空间的嵌入(embedding),也就是降维后的数据。在这个低维空间中,可以通过绘制散点图来可视化数据的结构和模式。
值得注意的是,虽然t-SNE可以很好地保持数据的局部结构,但它不保证保持数据的全局结构。也就是说,t-SNE降维后的结果可能会失去原始高维数据中的一些全局信息。此外,t-SNE的结果也可能受到随机初始化的影响,不同的运行可能会得到不同的结果。
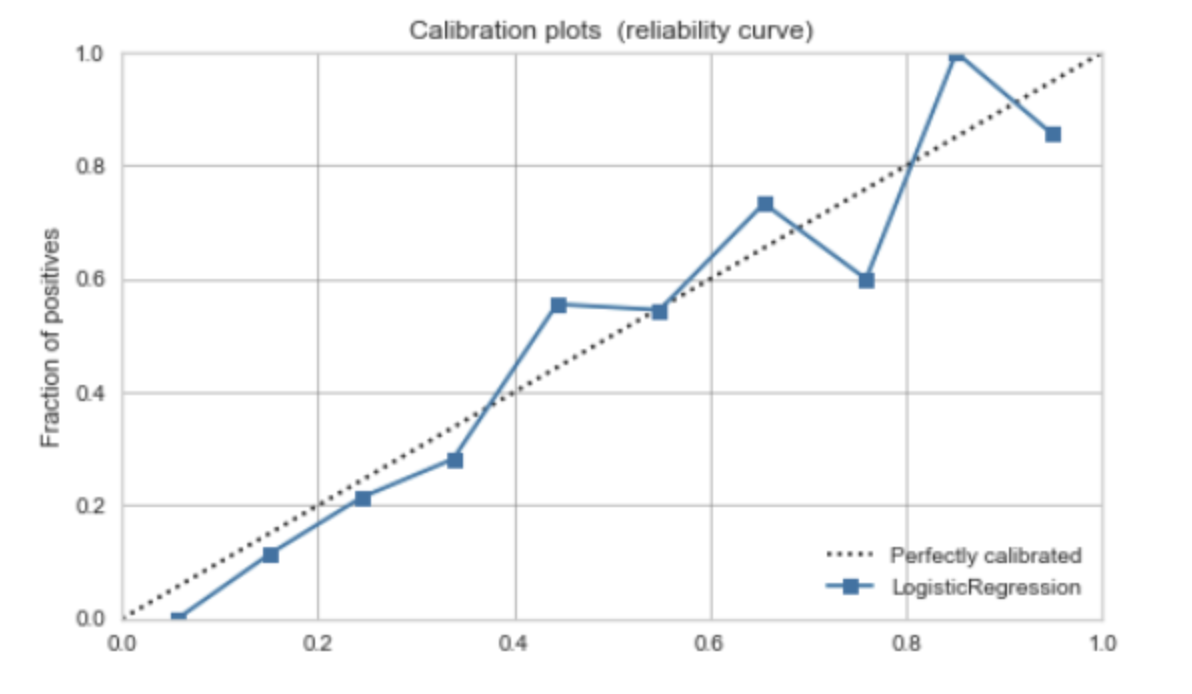
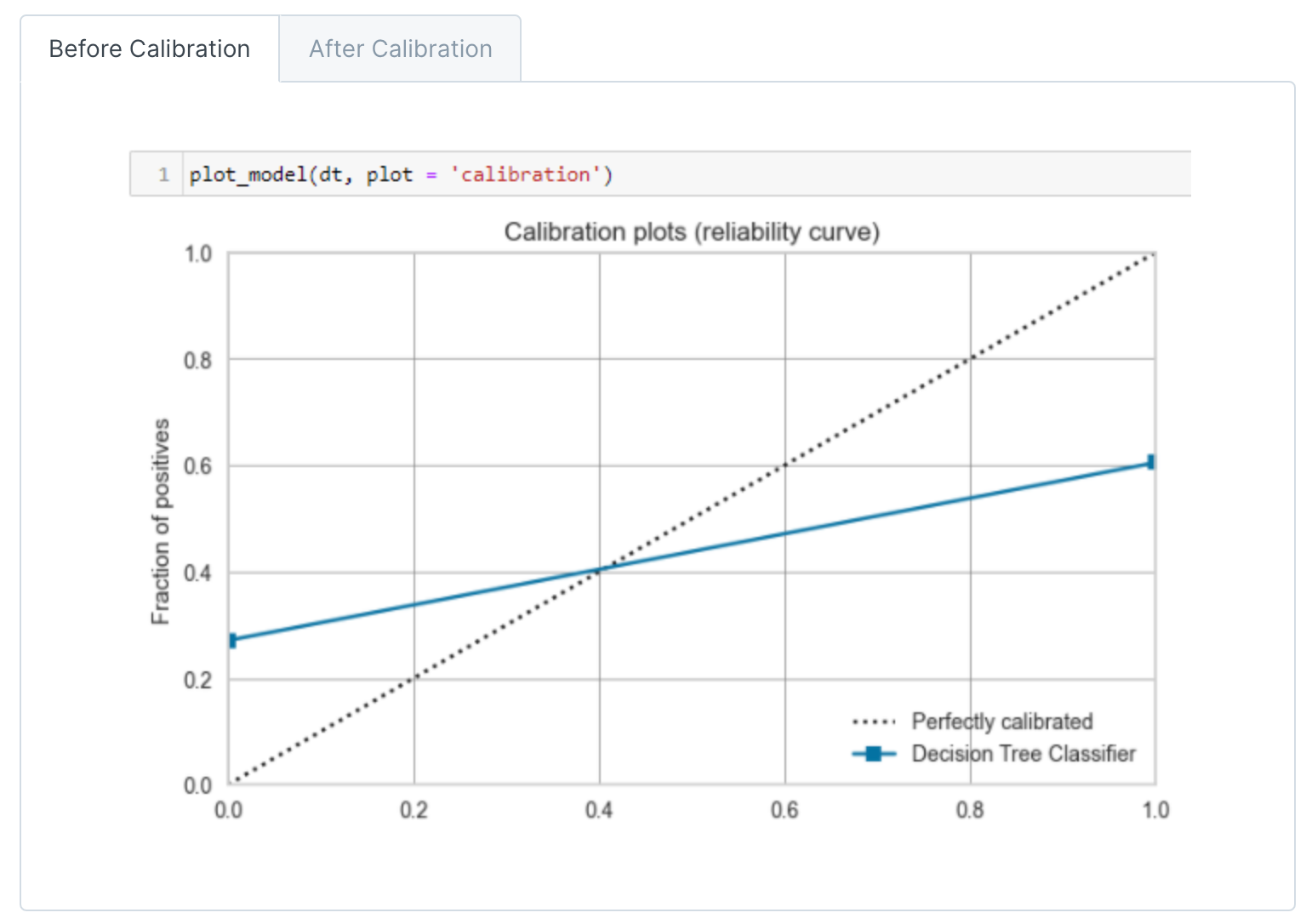
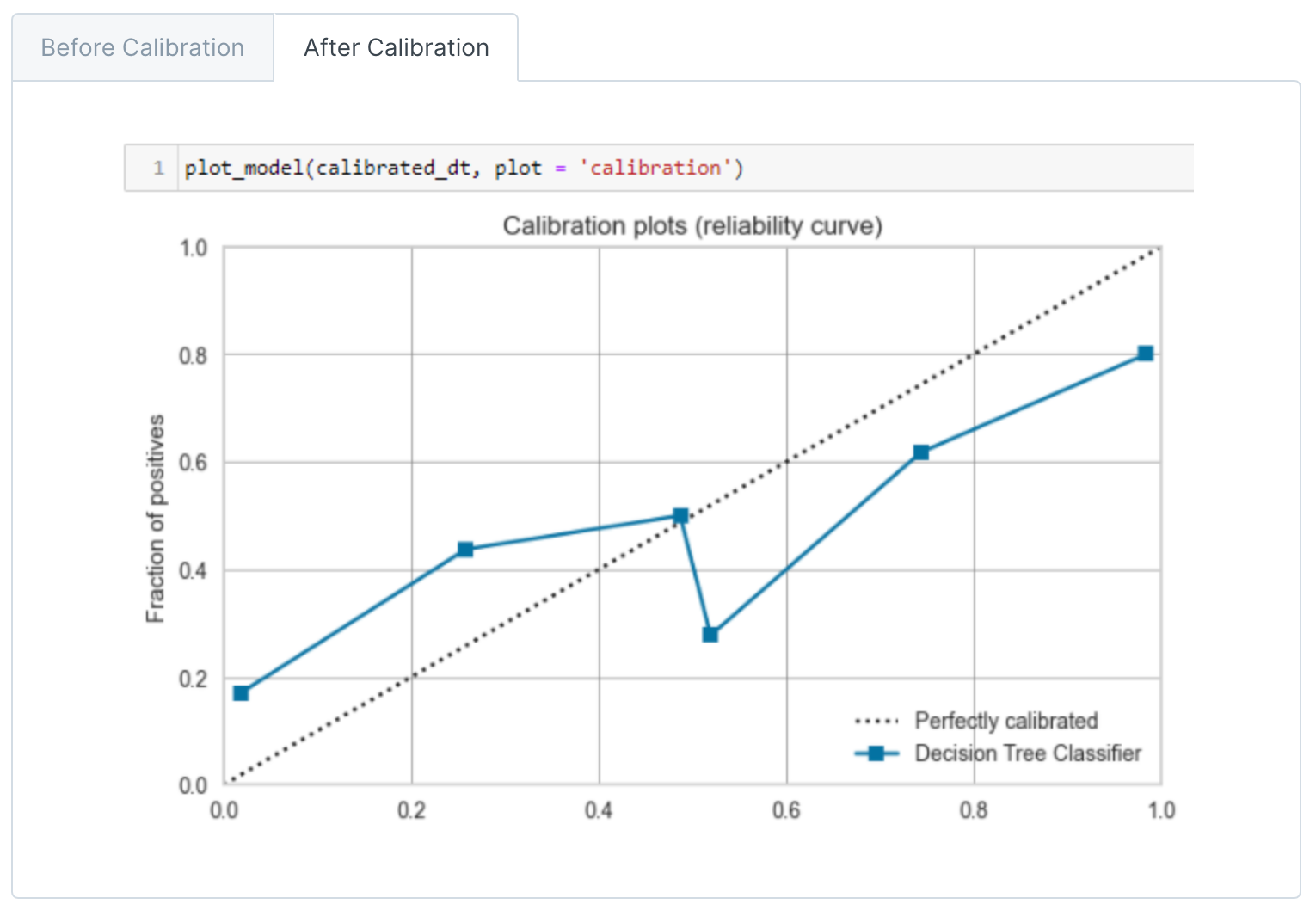
校准曲线(Calibration plots)或可靠性曲线(Reliability curve)是一种用于评估分类模型预测概率的可靠性的图形工具。在理想情况下,如果模型预测一个样本属于正类的概率是p,那么在所有模型预测为p的样本中,正好有p的比例是真正的正类。
在校准曲线中,横轴是预测的概率,纵轴是实际的概率。为了绘制校准曲线,首先需要将预测的概率分成几个区间(例如,0-0.1, 0.1-0.2, ..., 0.9-1.0),然后对于每个区间,计算所有落在该区间的样本的实际正类的比例。
如果模型的预测概率是完美校准的,那么校准曲线应该接近对角线。如果曲线在对角线之上,表示模型的预测概率偏低(模型过于保守);如果曲线在对角线之下,表示模型的预测概率偏高(模型过于乐观)。
校准曲线是评估模型预测概率质量的重要工具,特别是在那些需要概率输出的应用中,例如风险建模、疾病预测等。
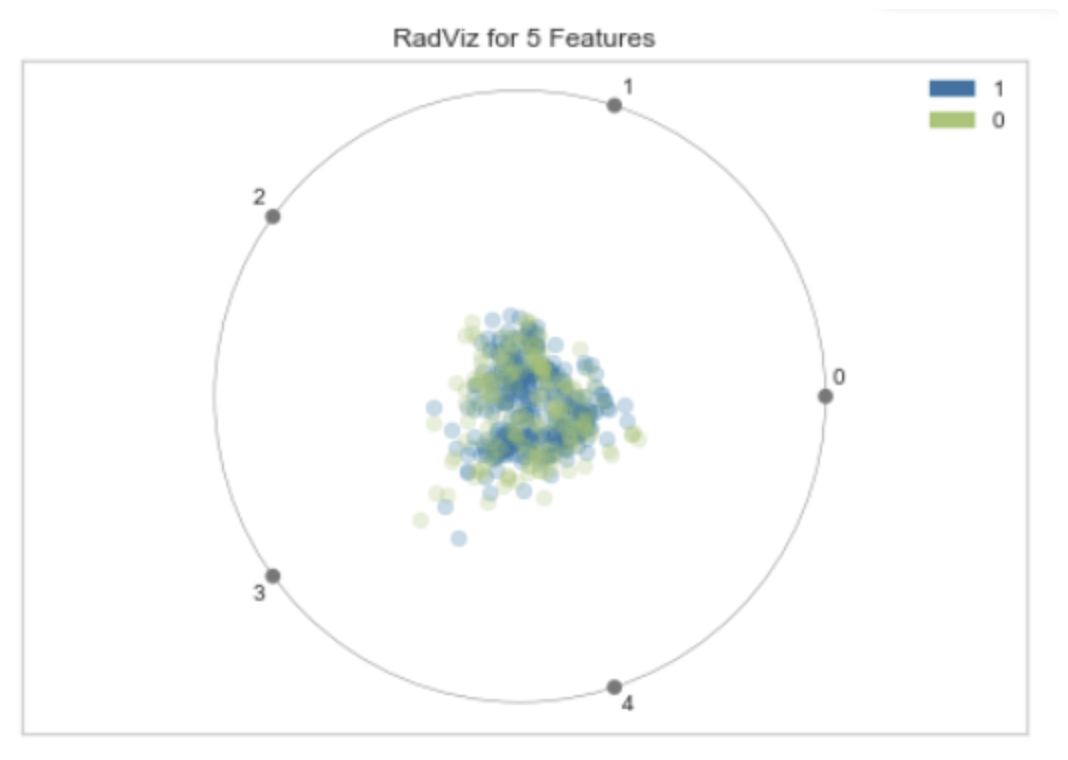
RadViz(Radial Visualization)是一种可视化高维数据的方法。它将每个特征放在一个单位圆的周围,然后将每个数据点表示为这些特征的加权平均位置。这种方法特别适合于可视化具有许多特征的数据集。
在 RadViz 图中,每个特征都在圆的边界上有一个锚点,数据点在圆内部,位置由其特征值决定。例如,如果一个数据点在所有特征上的值都相等,那么它将位于圆的中心。如果一个数据点在一个特征上的值远大于其他特征,那么它将靠近那个特征的锚点。
"RadViz for 5 Features" 可能是指使用 RadViz 方法可视化一个具有 5 个特征的数据集。在这种情况下,你会看到一个圆,圆的边界上有 5 个锚点,每个锚点代表一个特征,圆内的点代表数据。
RadViz 是一种强大的可视化工具,可以帮助我们理解数据的结构和特征之间的关系。然而,它也有一些局限性,例如,当特征数量很大时,RadViz 可能会变得混乱难以解读。
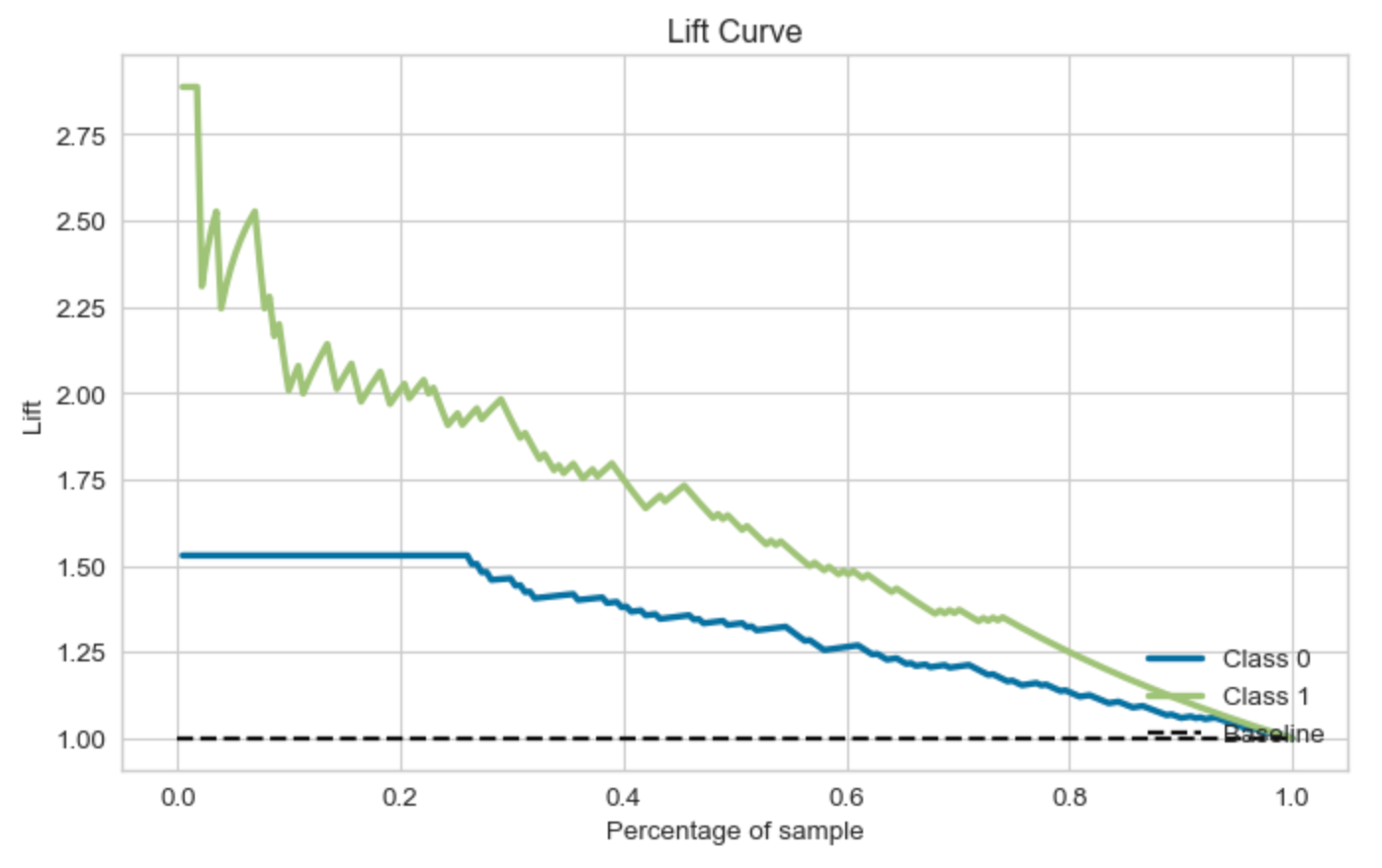
提升曲线(Lift Curve)是一种用于评估分类模型性能的工具,特别是在营销策略、风险评估等领域中,它可以帮助我们理解模型对于随机选择的增益。
提升曲线的横轴通常是预测为正类的样本的比例(按照预测概率从高到低排序),纵轴是真实为正类的样本的累积比例。例如,如果我们预测概率最高的10%的样本中有30%是真正的正类,那么在提升曲线上,当横轴为10%时,纵轴应为30%。
提升(Lift)是指模型找出正类样本的能力相对于随机选择的增益。在上述例子中,如果正类样本在总体中的比例是10%,那么模型的提升就是30%/10%=3。这意味着使用模型选择的效果是随机选择的3倍。
提升曲线可以帮助我们理解模型的性能,并决定如何最有效地使用模型。例如,在一个营销策略中,我们可能希望优先联系那些最有可能购买产品的客户。通过查看提升曲线,我们可以决定应该选择预测概率最高的多少比例的客户。
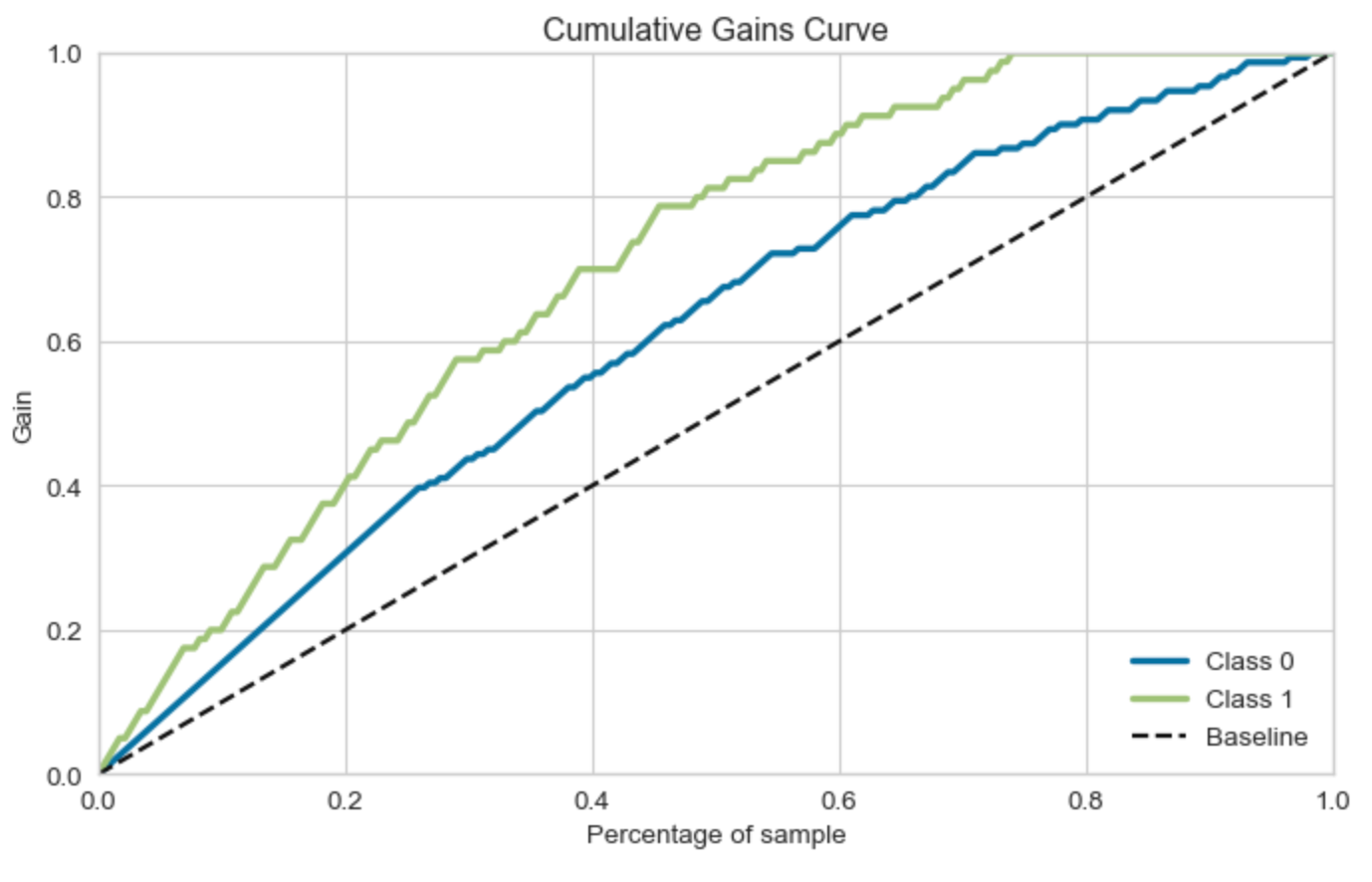
累积增益曲线(Cumulative Gains Curve)是一种用于评估分类模型性能的工具,特别是在营销策略和风险评估等领域。它可以帮助我们理解模型对于随机选择的增益。
在累积增益曲线中,横轴通常是预测为正类的样本的比例(按照预测概率从高到低排序),纵轴是真实为正类的样本的累积比例。例如,如果我们预测概率最高的10%的样本中有30%是真正的正类,那么在累积增益曲线上,当横轴为10%时,纵轴应为30%。
累积增益曲线可以帮助我们理解模型的性能,并决定如何最有效地使用模型。例如,在一个营销策略中,我们可能希望优先联系那些最有可能购买产品的客户。通过查看累积增益曲线,我们可以决定应该选择预测概率最高的多少比例的客户。
值得注意的是,累积增益曲线和提升曲线(Lift Curve)非常相似,它们都是用来评估模型性能的工具。然而,提升曲线更关注的是模型相对于随机选择的性能增益,而累积增益曲线更关注的是模型在不同的预测概率阈值下的性能。
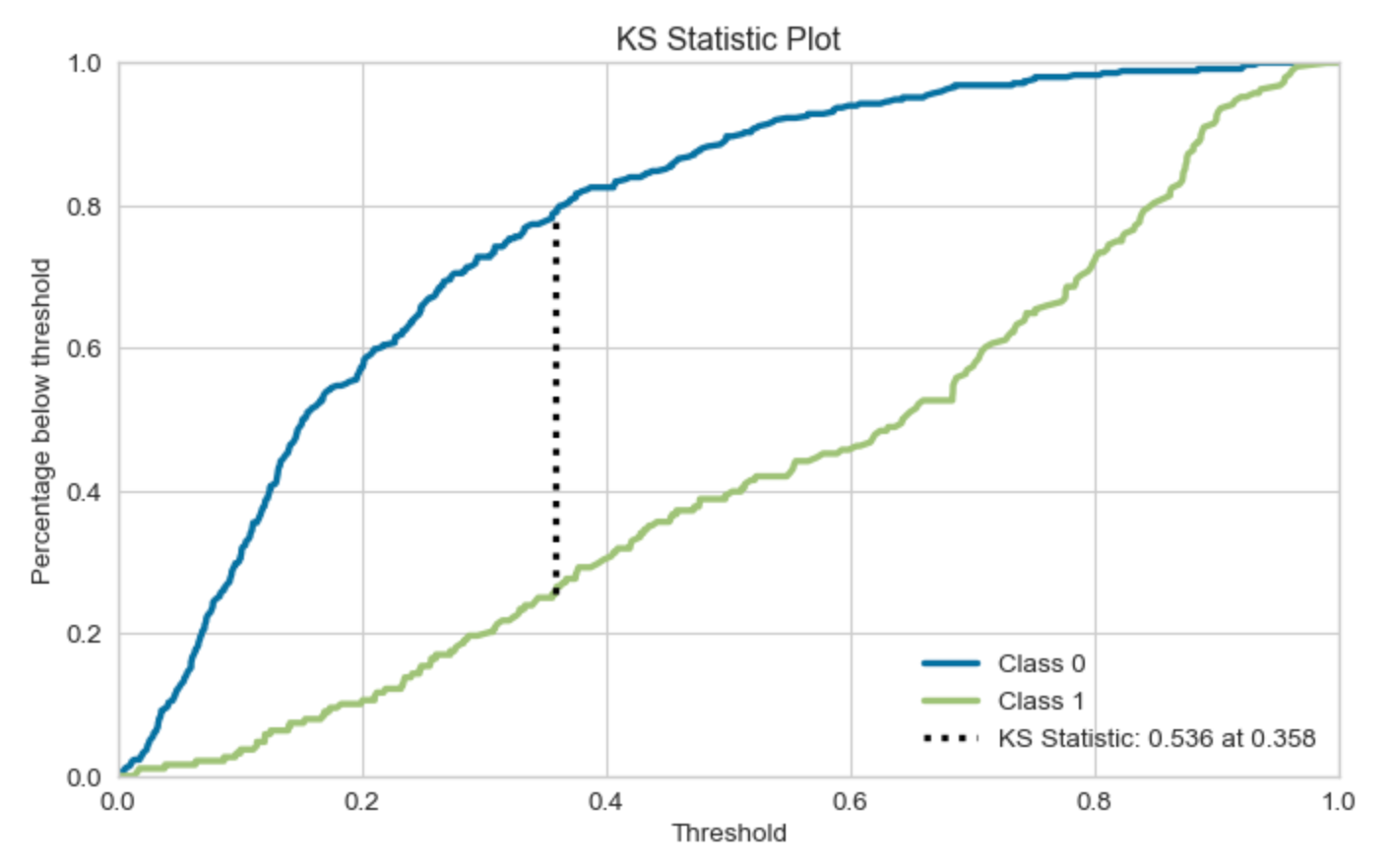
KS统计图(KS Statistic Plot)是一种用于评估二元分类模型性能的工具。KS代表Kolmogorov-Smirnov,它是一种衡量两个概率分布差异的统计量。
在二元分类问题中,KS统计图用于比较正类和负类的累积分布函数(CDF)。在KS统计图中,横轴通常是预测为正类的概率,纵轴是累积的正类和负类的比例。图中会有两条曲线,一条表示正类的CDF,一条表示负类的CDF。
KS统计量是正类和负类CDF之间的最大差距。在KS统计图中,这个差距就是两条曲线之间的最大垂直距离。KS统计量的值范围是0到1,值越大,表示模型的区分能力越强。
KS统计图可以帮助我们理解模型的性能,并找到最佳的概率阈值,以便在保证模型性能的同时,最大化模型的区分能力。
回归
- MAE (Mean Absolute Error): 这是实际值和预测值之间差的绝对值的平均值。它是一个用来衡量预测准确性的指标。MAE的值越小,说明预测模型拥有更好的精确度。
- MSE (Mean Squared Error): 这是实际值和预测值之间差的平方的平均值。MSE的值越小,说明预测模型拥有更好的精确度。但是,由于MSE是将差的平方进行平均,因此它对于较大的误差会给予更大的惩罚。
- RMSE (Root Mean Squared Error): 这是MSE的平方根。RMSE的值越小,说明预测模型拥有更好的精确度。RMSE和MSE的区别在于,RMSE的量纲(单位)与原始数据相同,而MSE的量纲是原始数据平方的单位。
- R2 (R-squared, Coefficient of Determination): 这是回归模型拟合优度的度量,表示模型解释目标变量变动的百分比。R2的值在0-1之间,值越接近1,说明模型的解释力度越好,预测性能越好。
- RMSLE (Root Mean Squared Logarithmic Error): 这是实际值和预测值的对数之间的差的平方的平均值的平方根。RMSLE对预测值和实际值的相对误差进行惩罚,因此当我们更关心预测值的百分比误差时,可以使用RMSLE。
- MAPE (Mean Absolute Percentage Error): 这是实际值和预测值之间的差的绝对值与实际值的比值的平均值。MAPE是一个百分比,用于衡量预测误差的相对大小。
示例:
观察点 预测值 实际值 1 10 12 2 8 6 3 6 7 4 15 14 我们现在计算这些评估指标:
- MAE (Mean Absolute Error):我们首先计算每个观察点的预测误差的绝对值,然后求平均:
观察点 预测误差 绝对误差 1 -2 2 2 2 2 3 -1 1 4 1 1 MAE = (2 + 2 + 1 + 1) / 4 = 1.5
- MSE (Mean Squared Error):我们首先计算每个观察点的预测误差的平方,然后求平均:
观察点 预测误差 误差平方 1 -2 4 2 2 4 3 -1 1 4 1 1 MSE = (4 + 4 + 1 + 1) / 4 = 2.5
- RMSE (Root Mean Squared Error):这是MSE的平方根,即 sqrt(2.5) = 1.58 (取两位小数)
- R² (R-squared):R²的计算比较复杂,需要我们计算模型的总平方和 (SST), 回归平方和 (SSR) 和 误差平方和 (SSE). 通常来说,我们需要一个基线模型(例如预测所有观察点的平均值)来计算SST和SSR。这里我们为简单起见,假设已知的R²值为0.8。
- MAPE (Mean Absolute Percentage Error):我们首先计算每个观察点的预测误差的绝对值与实际值的比值,然后求平均:
观察点 预测误差 绝对误差 绝对误差/实际值 1 -2 2 0.17 2 2 2 0.33 3 -1 1 0.
指标选择:
- R² (R-squared):如果你关心你的模型解释了多少数据的变异性,那么R²可能是一个好的选择。
- MAE (Mean Absolute Error) 和 RMSE (Root Mean Squared Error):这两种指标都可以衡量模型预测的准确性。如果你关心大的错误比小的错误更严重,那么RMSE可能是一个更好的选择,因为它对大的误差加权更重。如果你认为所有类型的错误都同样重要,那么MAE可能是一个更好的选择。
- MAPE (Mean Absolute Percentage Error):如果你的目标是比较不同规模的预测,例如预测销售额或库存需求,MAPE可以给出更直观的误差百分比。
- RMSLE (Root Mean Squared Logarithmic Error):如果你关心预测值和实际值的比例,而不仅仅是差异,或者你更关心预测低估的情况(因为它对低估的预测惩罚得更重),那么RMSLE可能是一个好的选择。
举个栗子:
假设你是一个房地产开发商,正在开发一个模型预测未来房价。你有两个模型:模型A和模型B,你需要判断哪一个更好。
假设在一组测试数据上,模型A和模型B的预测结果如下:
模型A:
- MAE: 10,000美元
- MSE: 500,000,000美元
- RMSE: 22,360美元
- R²: 0.8
模型B:
- MAE: 8,000美元
- MSE: 1,000,000,000美元
- RMSE: 31,620美元
- R²: 0.85
从MAE来看,模型B看起来更好,因为它的平均误差更小。但是,当我们看RMSE时,模型A的表现更好,这是因为RMSE对大的误差施加了更大的惩罚。
R²表明,模型B可以解释更多的价格变化,这意味着模型B可能更能理解房价的复杂动态。
现在选择哪个模型取决于你的业务需求。
如果你的目标是尽可能减小大的误差(例如,你不能承受预测价格太低的风险,因为这会导致严重的财务损失),那么你可能会选择RMSE低的模型A。
然而,如果你更关心模型能否捕获价格的波动和复杂性,那么你可能会选择R²更高的模型B。
这只是一个例子,实际情况可能会更复杂。重要的是理解每个指标的含义,并了解它们如何与你的具体需求相匹配。
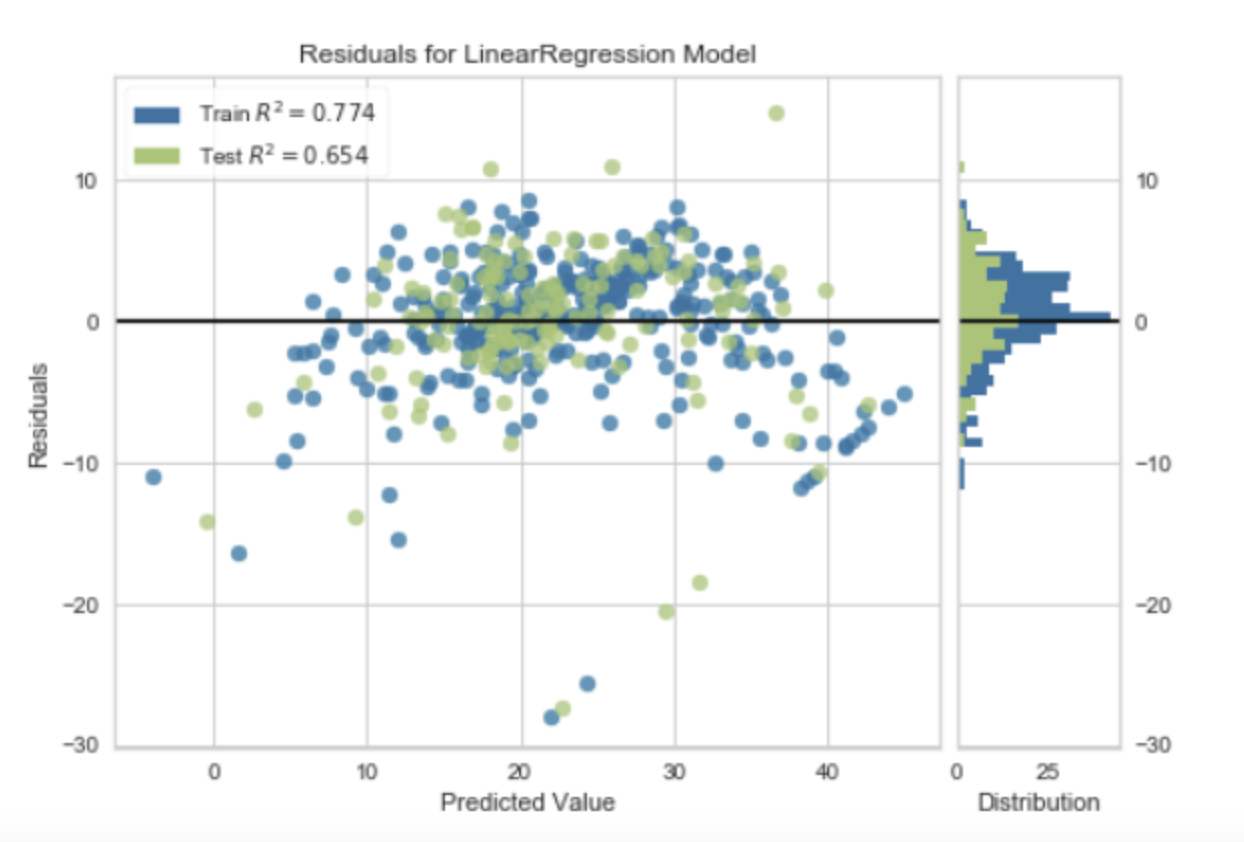
"Residuals for Linear Regression Model" 是指线性回归模型的残差,也就是模型预测值和实际观察值之间的差距。
在统计和机器学习中,残差是一个非常重要的概念。对于一个给定的数据点,模型的预测值和实际观察值之间的差异就是残差。在线性回归模型中,我们的目标就是最小化所有数据点的残差的平方和,这就是最小二乘法。
残差可以用来评估模型的性能。如果残差较小,说明模型的预测值接近实际观察值,模型的性能较好。如果残差较大,说明模型的预测值与实际观察值相差较大,模型的性能较差。
此外,残差的分布也可以提供模型性能的重要信息。理想情况下,线性回归模型的残差应该是随机分布的,也就是说,它们应该围绕0上下波动,没有明显的模式。如果残差有明显的模式(例如,随着预测值的增加或减小而系统性地增加或减小),那么这可能表明模型有偏差,需要进一步调整或改进。
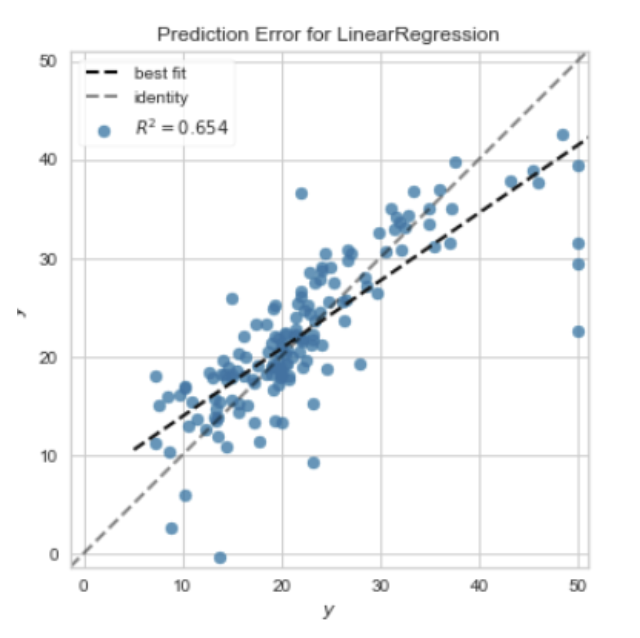
"Prediction Error for Linear Regression" 是指线性回归模型的预测误差,也就是模型预测值和实际观察值之间的差距。
预测误差是评估和比较模型性能的关键指标。对于一个给定的数据点,预测误差就是模型的预测值和实际观察值之间的差值。预测误差可以是正值或负值,取决于模型是否高估或低估了实际的结果。
预测误差可以用来评估模型的准确性。如果预测误差较小,说明模型的预测值接近实际观察值,模型的性能较好。如果预测误差较大,说明模型的预测值与实际观察值相差较大,模型的性能较差。
在实践中,我们通常会计算所有数据点的预测误差的平均值或者平方和(例如,均方误差)来得到一个总体的性能指标。此外,我们也可以绘制预测误差的分布或者预测值与实际值的散点图来更直观地理解模型的性能。
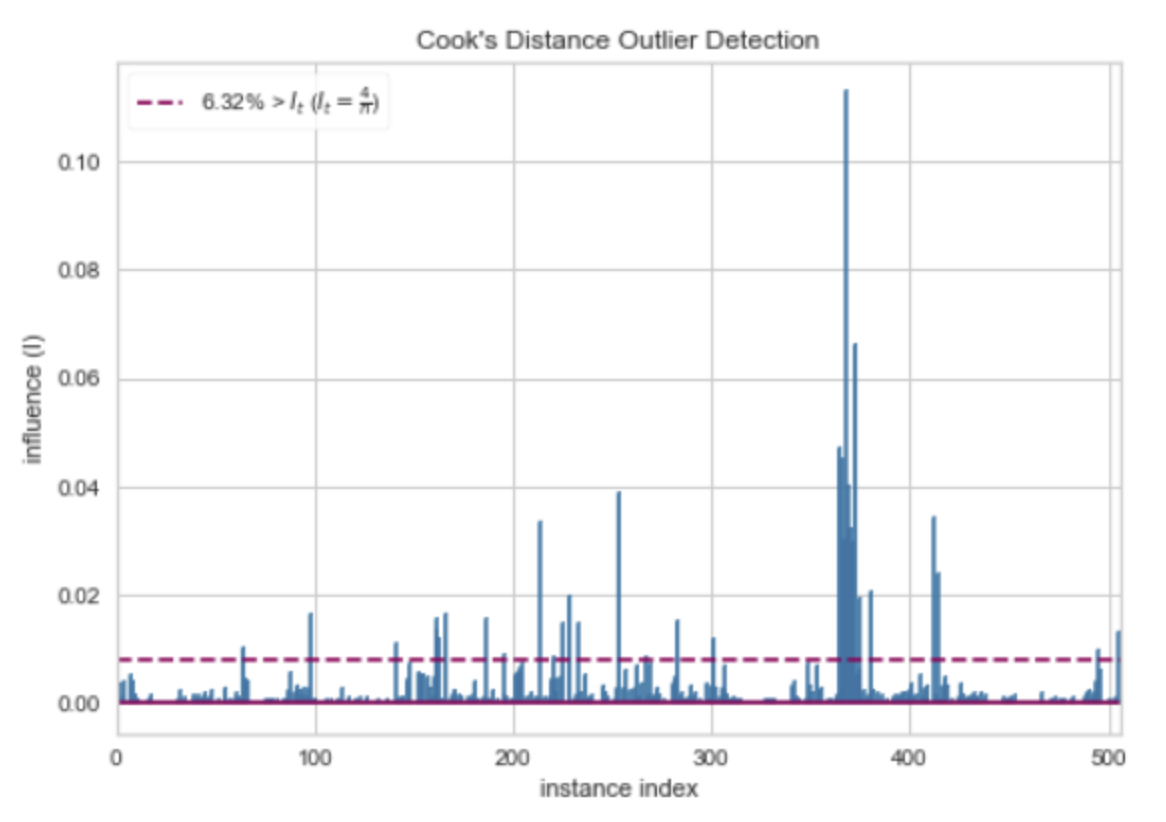
Cook's Distance是一种用于检测线性回归模型中离群值(outliers)的统计量。它衡量的是,当我们删除一个观测值并重新拟合模型时,模型参数估计值的变化程度。
Cook's Distance的计算公式为:
D_i = (e_i^2 * p) / (MSE * (1 - h_i)^2)
其中,e_i是第i个观测值的残差,p是模型的参数数量,MSE是模型的均方误差,h_i是第i个观测值的杠杆统计量(leverage statistic,衡量的是观测值对模型拟合的影响)。
Cook's Distance的值越大,表示第i个观测值对模型的影响越大,也就越可能是离群值。通常,如果Cook's Distance大于1,那么我们就会认为该观测值可能是离群值。
"Cook's Distance Outlier Detection"就是使用Cook's Distance来检测离群值的方法。这种方法可以帮助我们找出那些对模型影响较大的观测值,从而我们可以进一步研究这些观测值,看看它们是否是真正的离群值,或者是否存在数据质量问题等。
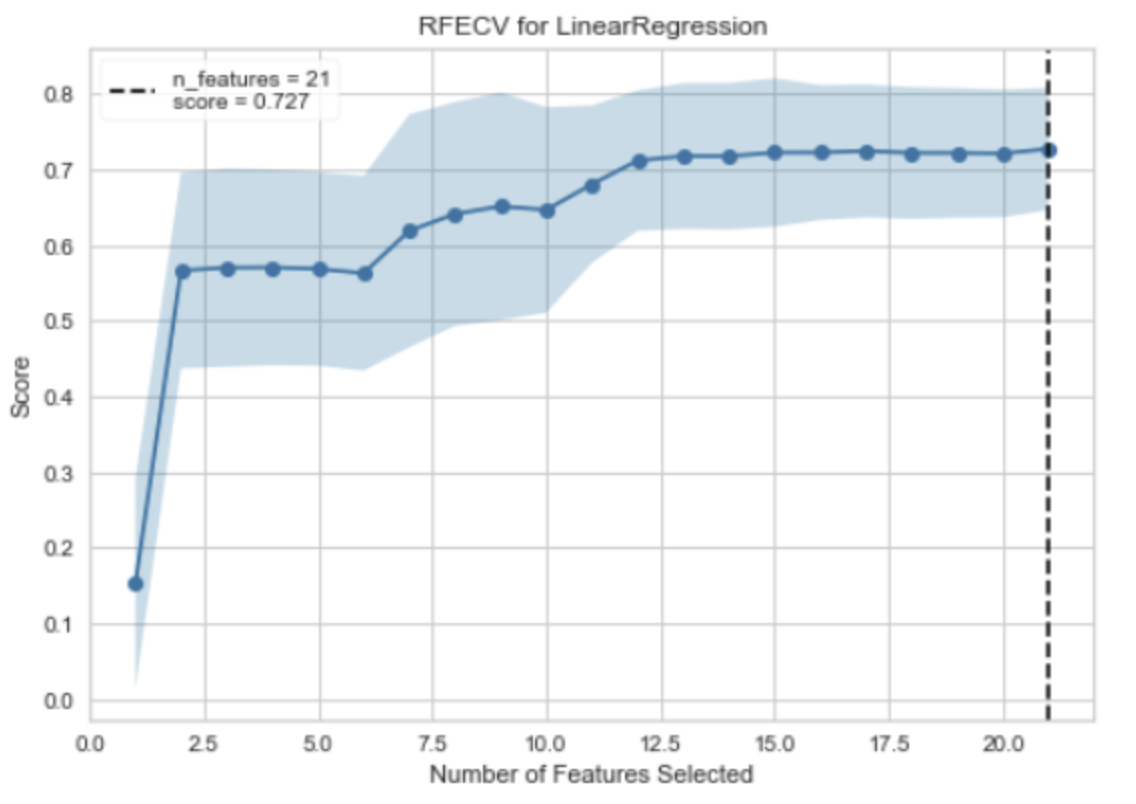
RFECV是 Recursive Feature Elimination with Cross-Validation(带交叉验证的递归特征消除)的缩写,它是一种特征选择方法,用于自动找出对模型预测最有贡献的特征。RFECV的工作原理是反复构建模型,然后选择出最好的(或最差的)特征(可以通过coef_属性或者feature_importances_属性来获取),把选出的特征放置一边,然后在剩余的特征上重复该过程,直到所有特征都遍历完。这个过程中使用的模型需要是能够提供重要性权重或系数的模型,如线性模型,SVM,决策树等。当你看到 "RFECV for LinearRegression" 时,它通常意味着使用带交叉验证的递归特征消除方法来选择线性回归模型的特征。这个过程可以帮助我们找出对线性回归模型预测最有贡献的特征,从而提高模型的性能或者解释性。
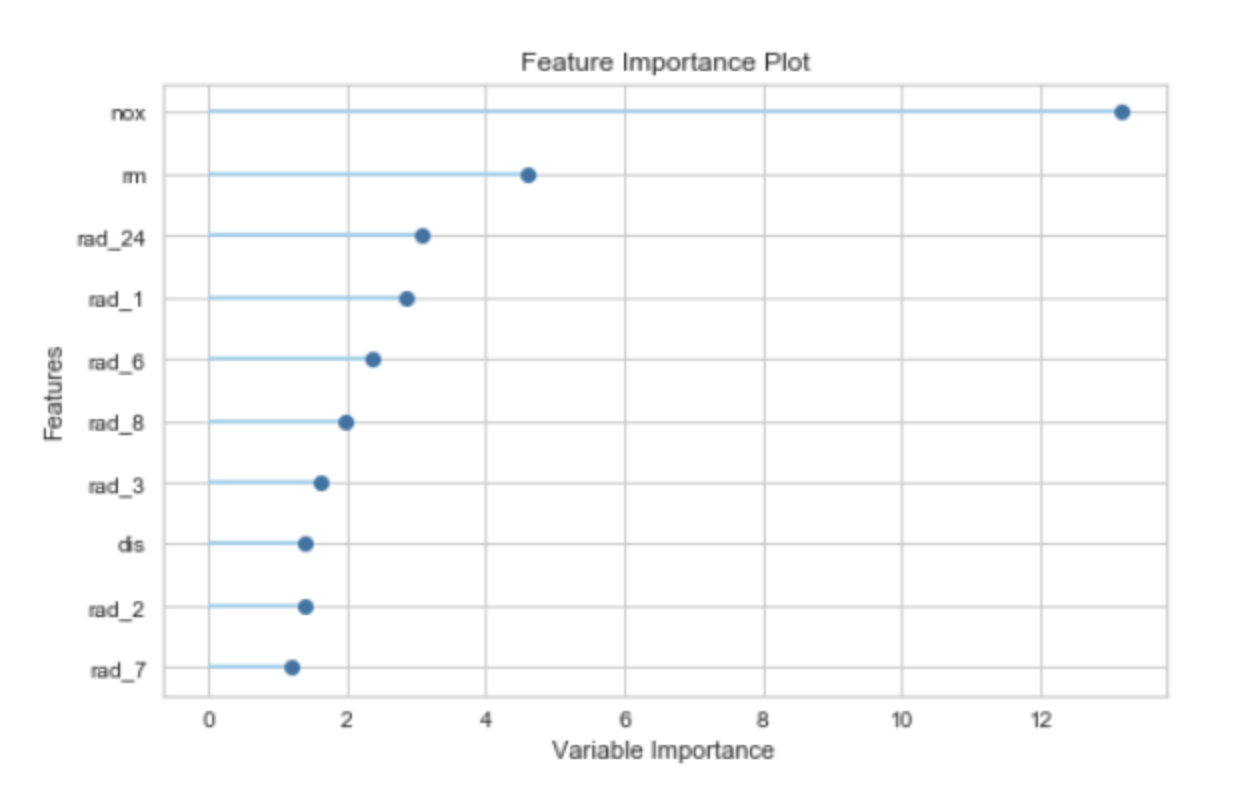
特征重要度(Feature Importance)是一种用于解释机器学习模型的技术,它为输入特征分配一个分数,以表示每个特征对模型预测的贡献大小。特征重要度可以帮助我们理解哪些特征对模型的预测最有影响,从而提供模型的可解释性。
特征重要度的计算方法取决于具体的模型类型。例如:
- 对于决策树模型,特征重要度通常是根据特征在树中的分裂点出现的频率和深度来计算的。一个特征如果在树的顶部(深度较小)并且在多个树中频繁出现,那么它通常被认为是重要的。
- 对于线性模型,特征的系数可以被视为特征重要度。系数的绝对值越大,特征越重要。
- 对于基于梯度提升的模型(如 XGBoost 或 LightGBM),特征重要度可以是基于特征分裂增益的总和,或者是特征被选为分裂点的次数。
值得注意的是,特征重要度只能提供特征和目标变量之间的关系的相对度量,并不能提供特征和目标之间的确切关系(例如,它不能告诉你改变一个特征的值会如何精确地改变预测结果)。此外,特征重要度也不能很好地处理相关特征。如果两个特征高度相关,那么它们的重要度可能会被模型任意分配。
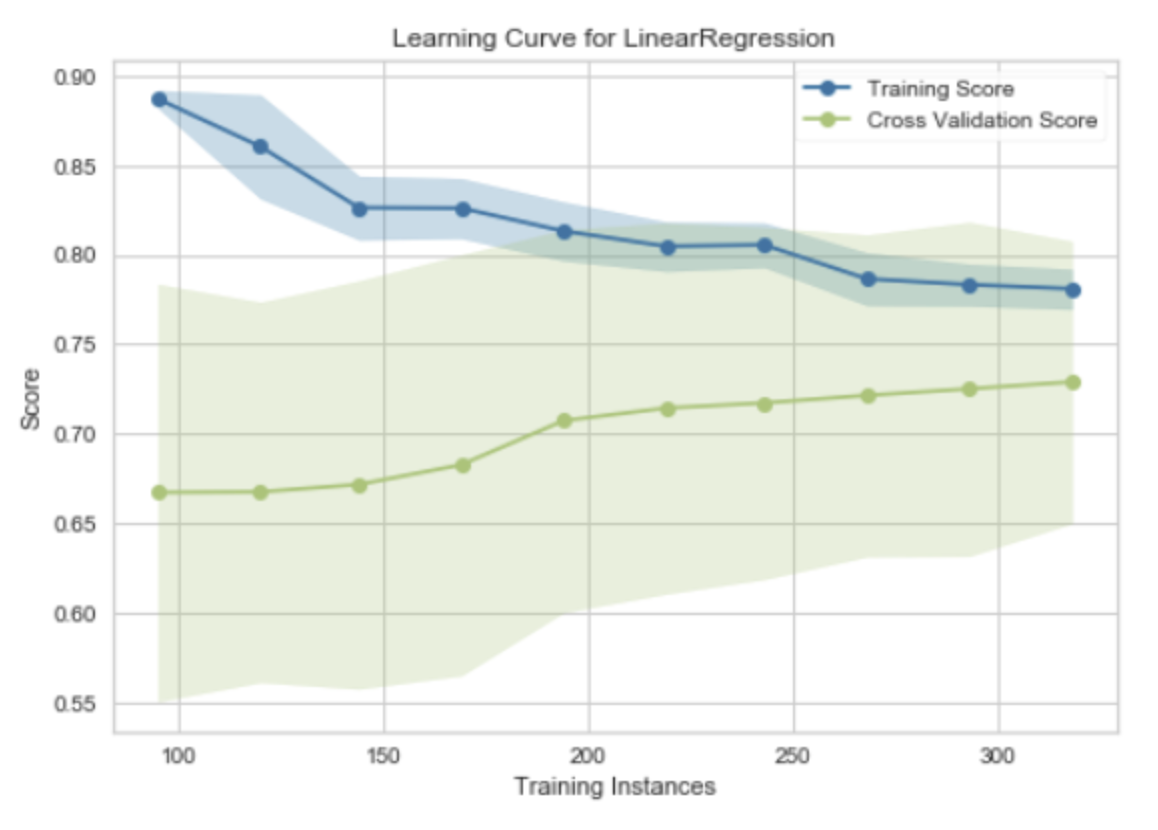
"Learning Curve for Logistic Regression" 是一种用于评估逻辑回归模型性能的工具。学习曲线(Learning Curve)是一种图形,它展示了模型在训练集和验证集(或测试集)上的性能随着训练样本数量的增加而变化的情况。
在学习曲线中,横轴通常是训练样本的数量,纵轴是模型的性能度量,如准确率、损失函数的值等。对于逻辑回归模型,学习曲线可以帮助我们理解更多的训练数据是否能够提高模型的性能。
学习曲线有两条线,一条表示训练误差,另一条表示验证误差:
- 训练误差:这是模型在训练数据上的误差。随着训练样本数量的增加,训练误差通常会增加,因为模型需要拟合更多的数据。
- 验证误差:这是模型在验证数据上的误差。随着训练样本数量的增加,验证误差通常会减少,因为模型得到了更多的信息来学习数据的模式。
通过观察学习曲线,我们可以得到一些关于模型性能的见解,例如,如果训练误差和验证误差之间的差距很大,可能说明模型过拟合;如果两者都很高,可能说明模型欠拟合。
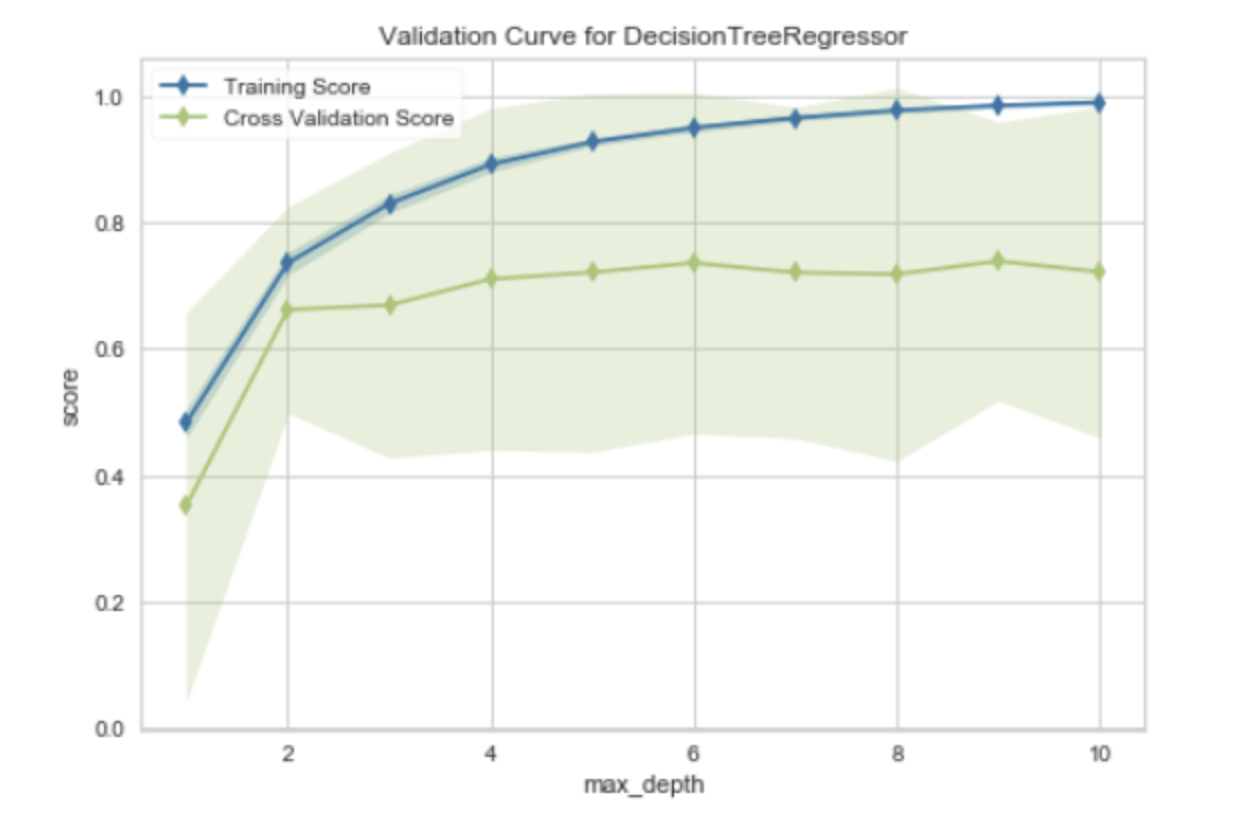
"Validation Curve for Logistic Regression" 是一种用于评估逻辑回归模型性能的工具。验证曲线(Validation Curve)是一种图形,它展示了模型在训练集和验证集(或测试集)上的性能随着模型参数的变化而变化的情况。
在验证曲线中,横轴通常是某个模型参数的值,纵轴是模型的性能度量,如准确率、损失函数的值等。对于逻辑回归模型,验证曲线可以帮助我们理解不同的参数值如何影响模型的性能。
验证曲线有两条线,一条表示训练得分,另一条表示验证得分:
- 训练得分:这是模型在训练数据上的得分。随着模型复杂度的增加(例如,参数值的增加),训练得分通常会增加,因为模型能够更好地拟合训练数据。
- 验证得分:这是模型在验证数据上的得分。随着模型复杂度的增加,验证得分通常先增加后减少。这是因为当模型过于复杂时,它可能会过拟合训练数据,导致在未见过的验证数据上的性能下降。
通过观察验证曲线,我们可以找到模型性能最好的参数值,也可以了解模型是否过拟合或欠拟合。
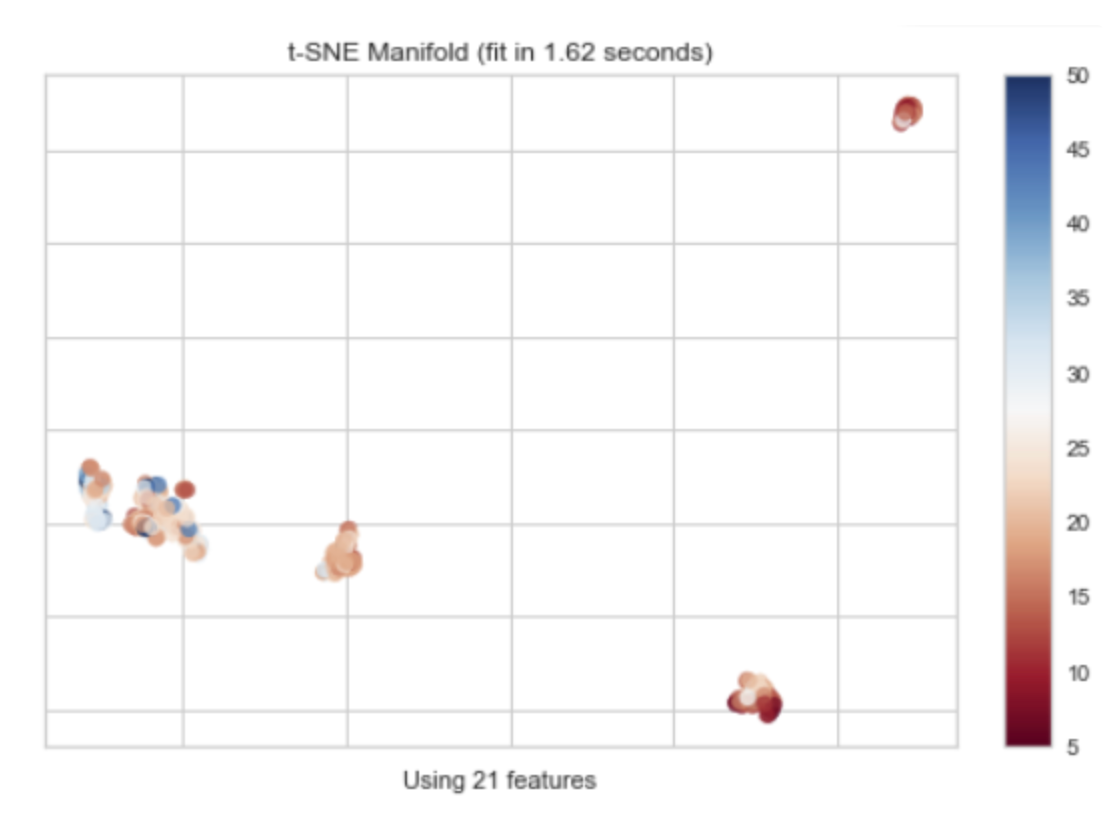
t-SNE(t-Distributed Stochastic Neighbor Embedding)是一种用于数据可视化的工具,特别适用于高维数据的降维和可视化。它是一种非线性的降维方法,可以保持原始高维数据中的局部结构。
t-SNE的工作原理是在高维空间和低维空间(通常是2D或3D,以便于可视化)中都定义一个概率分布,使得相似的对象有更高的概率被选择为邻居。然后,t-SNE优化这两个概率分布的KL散度(Kullback-Leibler divergence),使得低维空间中的概率分布尽可能接近高维空间中的概率分布。
"t-SNE Manifold"通常指的是使用t-SNE方法得到的低维空间的嵌入(embedding),也就是降维后的数据。在这个低维空间中,可以通过绘制散点图来可视化数据的结构和模式。
值得注意的是,虽然t-SNE可以很好地保持数据的局部结构,但它不保证保持数据的全局结构。也就是说,t-SNE降维后的结果可能会失去原始高维数据中的一些全局信息。此外,t-SNE的结果也可能受到随机初始化的影响,不同的运行可能会得到不同的结果。
聚类

- Silhouette Coefficient(轮廓系数): 这是一种解释和验证数据集中的聚类的方法。轮廓系数的值范围在-1到1之间,较高的值表示样本与其所在的聚类更匹配,并且与相邻聚类的匹配程度较低,因此高的轮廓系数可以认为是好的聚类。
- Calinski-Harabasz Index(Calinski-Harabasz指数):也称作方差比标准。它通过比较聚类之间和聚类内部的离散程度来评估聚类的效果。值越大,说明聚类效果越好。
- Davies-Bouldin Index(Davies-Bouldin指数): 是一种评估聚类质量的指标,它基于聚类内部的平均距离和聚类之间的距离之比。较小的Davies-Bouldin指数通常会得到更好的聚类效果。
- Homogeneity(同质性): 如果聚类中的每个群集只包含一个类的样本,那么我们称聚类结果为同质的。其值在0-1之间,值越大,同质性越好。
- Rand Index(Rand指数): Rand Index衡量的是我们的聚类结果与实际情况的吻合度,值范围在0-1之间,越大表示聚类效果越好。
- Completeness(完整性): 如果同一类的样本都被分到同一个群集中,那么我们称聚类结果具有完整性。其值在0-1之间,值越大,完整性越好。
这些度量方法各有优点和缺点,应选择哪种度量方法取决于你的具体需求和问题的性质。
- Silhouette Coefficient(轮廓系数)
- 优点:轮廓系数为每个样本提供了一个一致和简明的图形表示,可以帮助解释聚类结果。
- 缺点:当聚类形状复杂或者聚类数目过多时,可能无法得到很好的结果。
- 使用场景:适用于对聚类结果进行解释和可视化。
- Calinski-Harabasz Index(Calinski-Harabasz指数)
- 优点:比较简单,计算效率高。越大越好,直观易理解。
- 缺点:对于非凸形状的数据或者噪声敏感。
- 使用场景:适用于大规模数据集的聚类质量评估。
- Davies-Bouldin Index(Davies-Bouldin指数)
- 优点:计算简单,直观易理解,较小的值表示更好的聚类效果。
- 缺点:可能会偏向于生成更多的聚类,因为较小的值通常意味着聚类之间有更大的距离。
- 使用场景:适用于需要评估聚类分离度的任务。
- Homogeneity(同质性)
- 优点:直观易理解,值越大表示同质性越好。
- 缺点:只关注聚类的同质性,忽略了聚类的完整性。
- 使用场景:适用于需要评估聚类同质性的任务。
- Rand Index(Rand指数)
- 优点:直观易理解,对于噪声和聚类数量的变化相对稳定。
- 缺点:可能会偏向于较大的聚类数量。
- 使用场景:适用于有真实标签,并且需要评估聚类结果与真实标签一致性的任务。
- Completeness(完整性)
- 优点:直观易理解,值越大表示完整性越好。
- 缺点:只关注聚类的完整性,忽略了聚类的同质性。
- 使用场景:适用于需要评估聚类完整性的任务。
在实际应用中,可能需要结合多种指标以及对问题的理解来评估聚类结果的好坏。
假设我们有6个数据点(A, B, C, D, E, F),我们的目标是将这些点聚类。
我们有两个聚类模型:
模型1的聚类结果是:聚类1 = {A, B, C}, 聚类2 = {D, E, F}
模型2的聚类结果是:聚类1 = {A, B, C, D}, 聚类2 = {E, F}
我们的实际(或“正确的”)聚类是:实际聚类1 = {A, B, D}, 实际聚类2 = {C, E, F}
现在,我们来看看模型1和模型2在这些指标下的表现:
- 同质性(Homogeneity):如果一个给定的聚类只包含单一类的数据点,那么我们可以说这个聚类是同质的。在这个例子中,模型1和模型2都满足同质性的要求,因为它们的每个聚类都只包含一种类别的数据点。
- 完整性(Completeness):如果给定类的所有数据点都分配到同一个聚类中,那么我们可以说这个聚类是完整的。在这个例子中,模型1和模型2都满足完整性的要求,因为它们的每个类都只分配到一个聚类中。
- Rand指数(Rand Index):这个指标衡量的是我们的聚类结果与实际情况的吻合度。在这个例子中,模型1的聚类结果与实际聚类完全一致,所以其Rand指数为1。而模型2的聚类结果与实际聚类有所偏差(因为D被错误地分配到了聚类1,而实际上它应该在聚类2),所以其Rand指数会小于1。
- 轮廓系数(Silhouette Coefficient):该系数计算的是聚类的密集程度和分离程度之间的平衡。如果一个数据点与同一聚类中的其他数据点非常接近,而与其他聚类中的数据点非常远离,那么这个数据点的轮廓系数将接近1。具体的数值将取决于数据点在空间中的分布,我们在这个简化的例子中无法直接计算。
- Calinski-Harabasz指数和Davies-Bouldin指数:这两个指标也需要数据点在空间中的具体分布,所以我们也无法在这个简化的例子中直接计算。
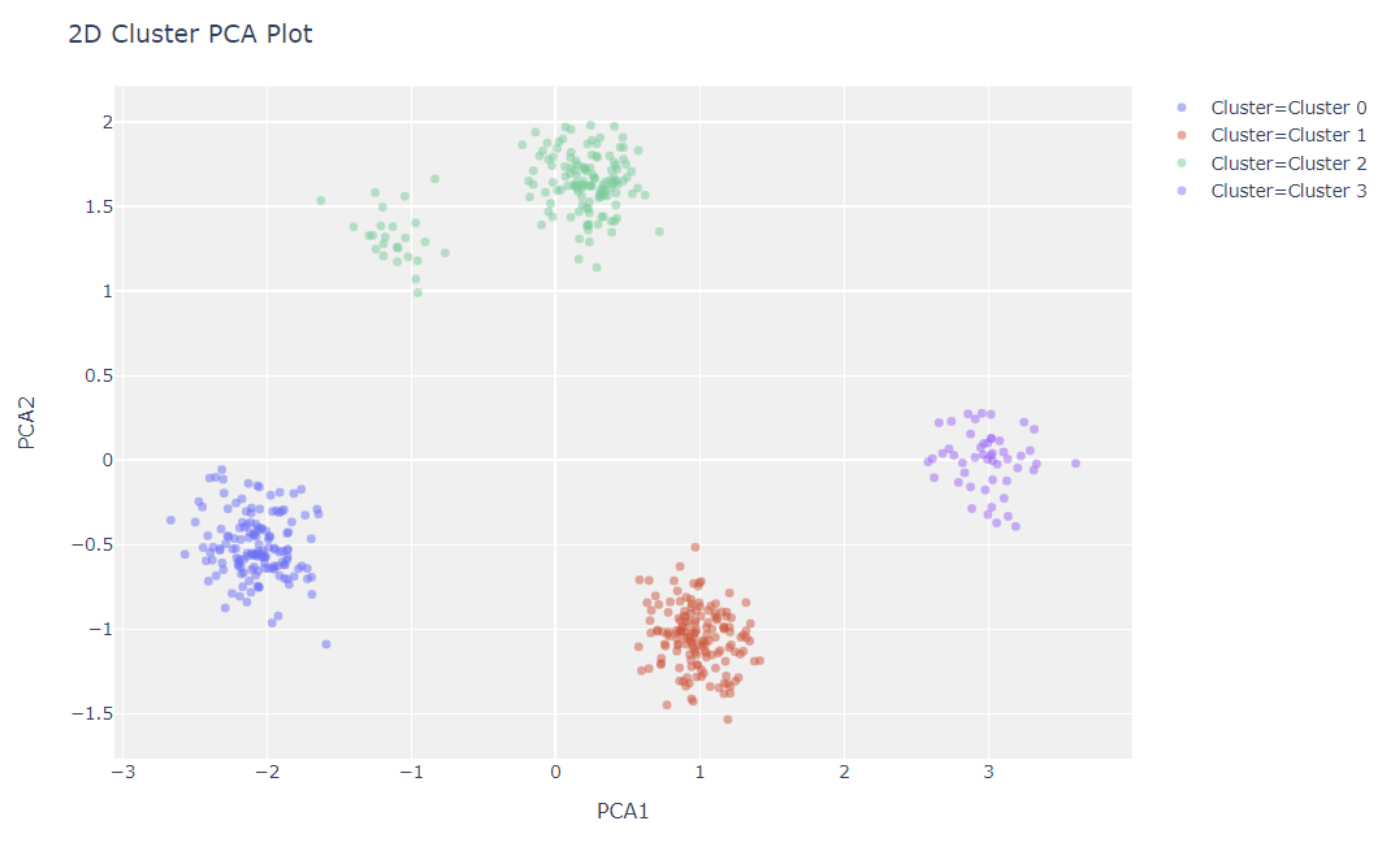
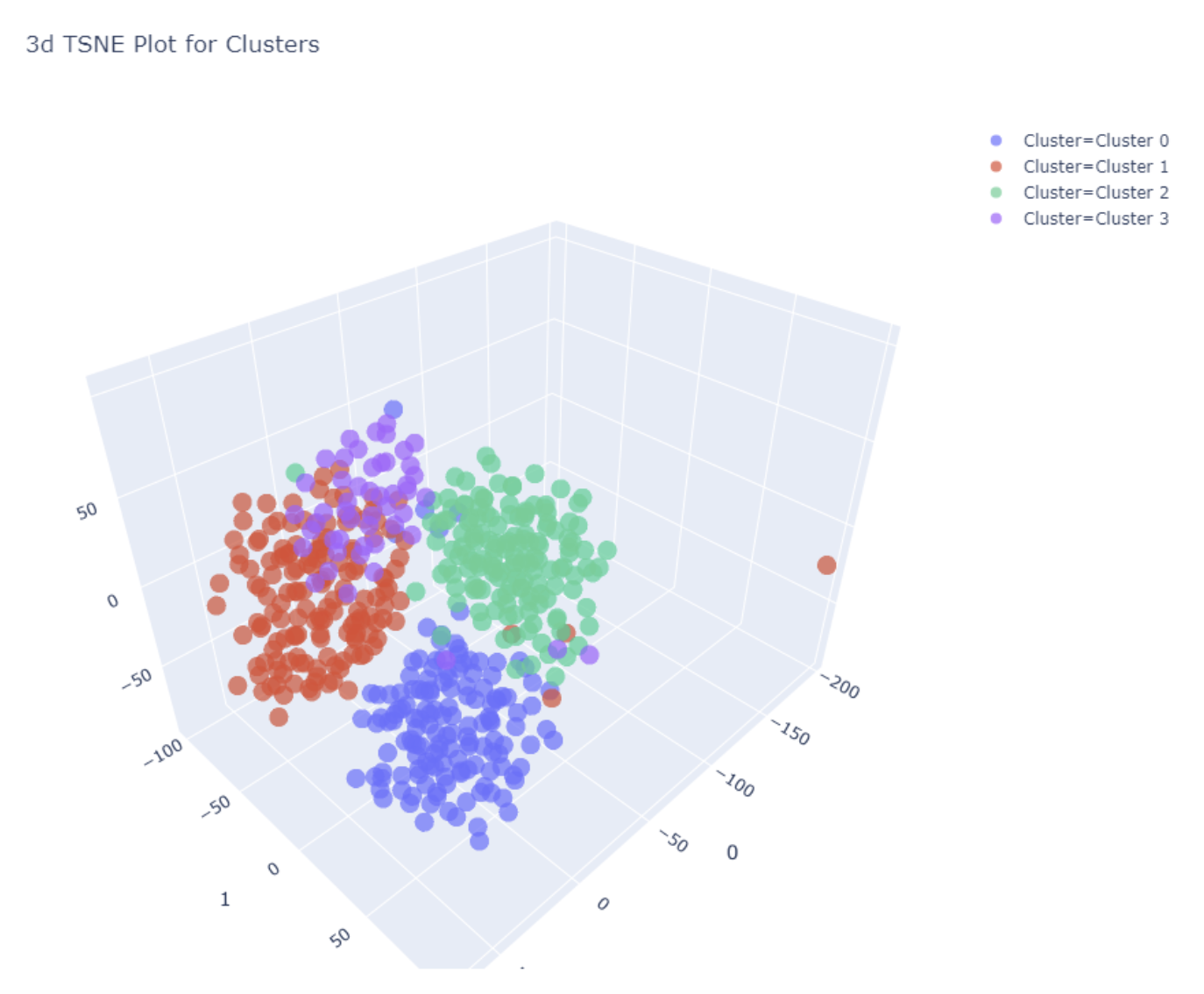
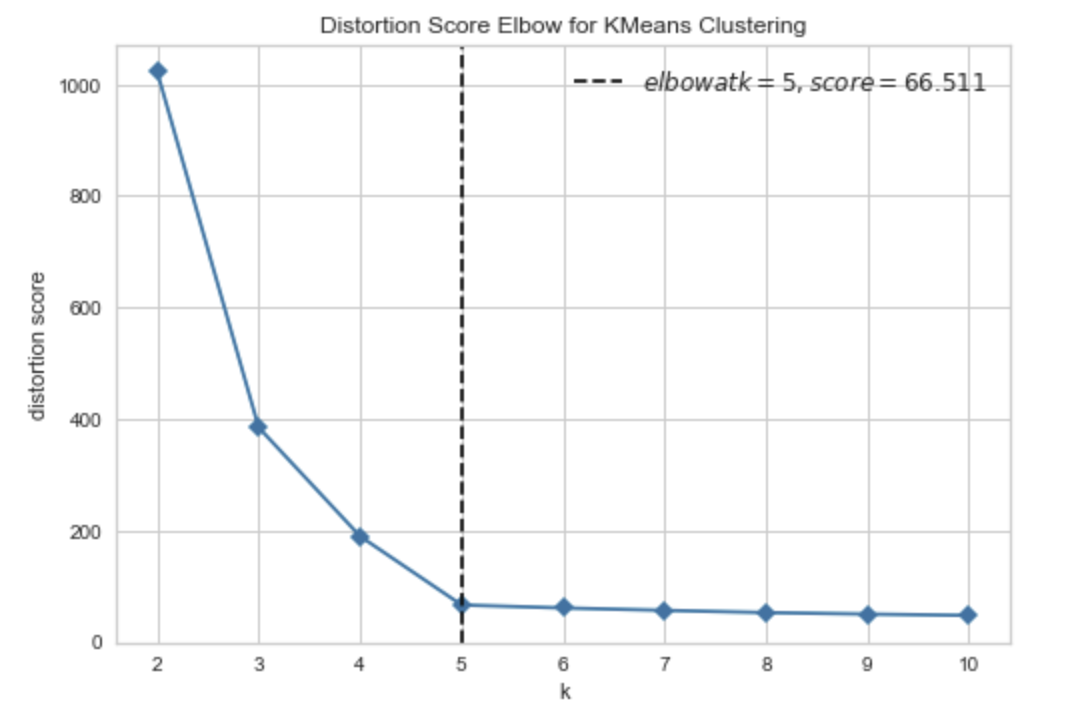
"Distortion Score Elbow for KMeans Clustering"是一种用于评估k-means聚类模型性能的工具。
在k-means聚类中,我们需要选择k值(聚类数),以便将样本划分为k个聚类。一个常用的方法是通过计算每个聚类内部的平均距离(也称为畸变程度)来评估聚类的性能。如果畸变程度较小,则说明聚类效果较好。
Distortion Score Elbow是一种通过可视化畸变程度的变化来帮助我们选择k值的方法。在这种方法中,我们计算不同k值下的畸变程度,并将这些值绘制成一条曲线。然后,我们观察曲线的形状,找到一个“拐点”,该拐点表示k值的选择可以使畸变程度显著降低,同时保持聚类的效果。
一般来说,Distortion Score Elbow通常是一个“手肘形状”的曲线,因为曲线的斜率在拐点处会发生变化。拐点通常是k值的一个合理选择,但不一定是最佳选择,因为有时候拐点不太明显,或者我们更关心其他方面的性能度量(如轮廓系数)。
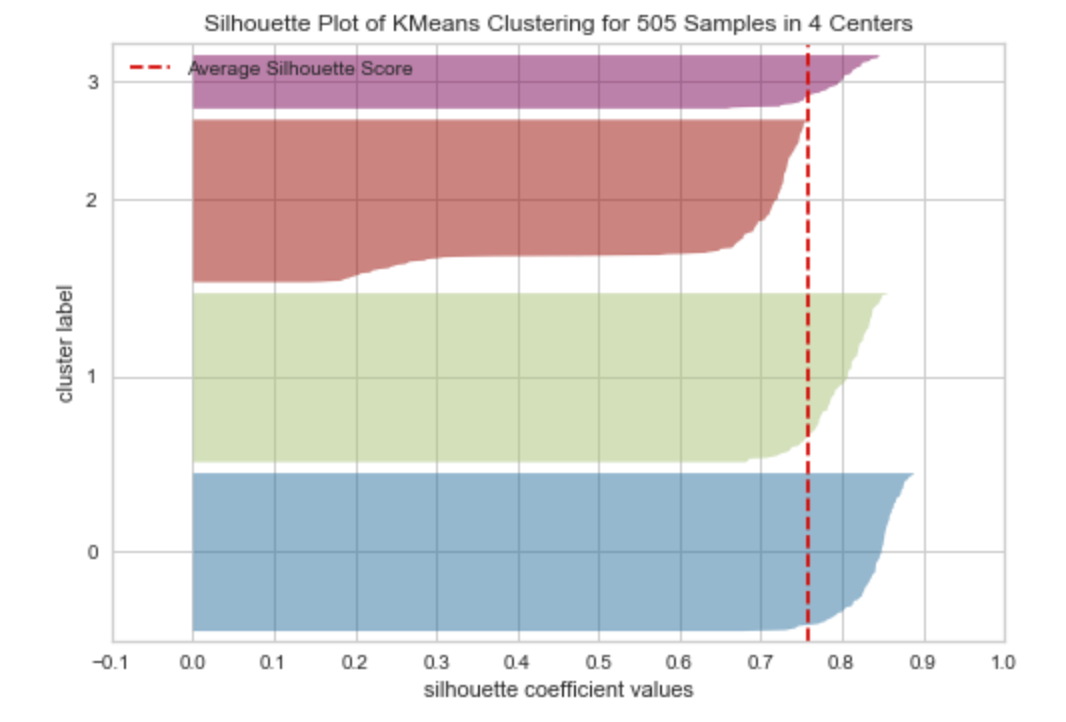
"Silhouette Plot of KMeans Clustering for 505 Samples in 4 Centers"是一种用于评估K-means聚类模型性能的工具。
在k-means聚类中,我们需要选择k值(聚类数),以便将样本划分为k个聚类。一般来说,我们希望每个聚类内部的样本相似度较高,不同聚类之间的样本相似度较低。Silhouette Plot可以帮助我们理解每个样本在聚类中的相似度和不相似度。
Silhouette Plot的横轴是样本的Silhouette系数,纵轴是每个样本在聚类中的编号。Silhouette系数是一个介于-1和1之间的值,表示样本在聚类中的相似度。如果Silhouette系数越接近1,表示样本在聚类中的相似度越高;如果Silhouette系数越接近-1,表示样本在聚类中的相似度越低;如果Silhouette系数接近0,则表示样本在聚类中的相似度差不多。
通过观察Silhouette Plot,我们可以得到一些关于聚类的见解。例如,如果大部分样本的Silhouette系数都接近1,则表示聚类效果很好;如果有一些样本的Silhouette系数接近-1,则可能说明这些样本应该分到其他聚类中;如果大部分样本的Silhouette系数都接近0,则可能说明聚类效果不太好,或者有些样本不太适合用K-means聚类。
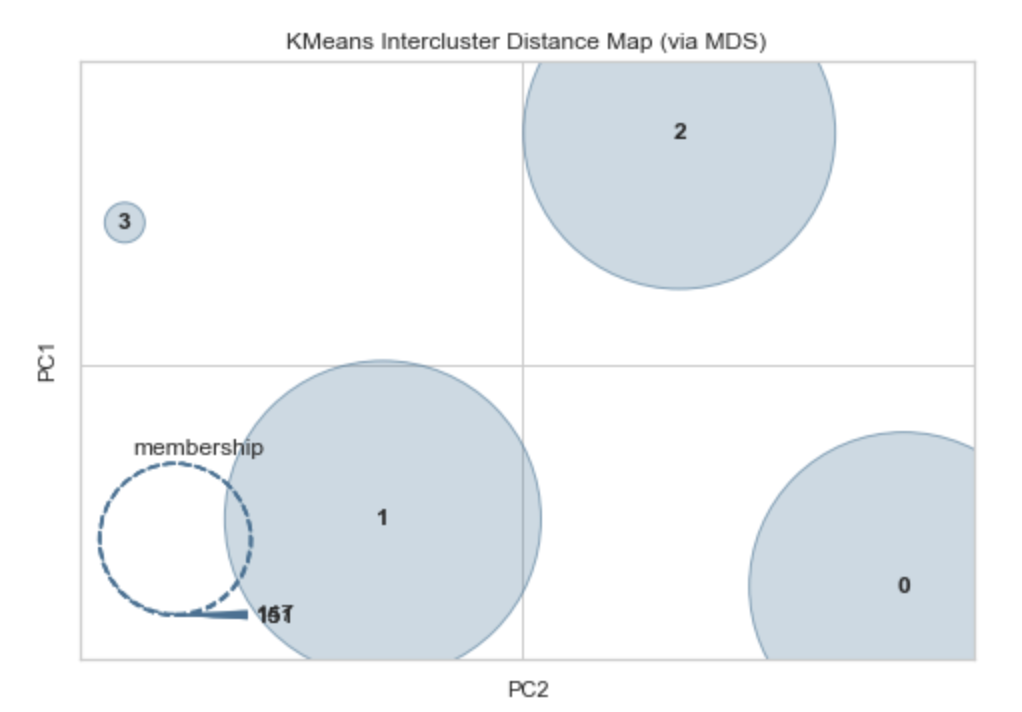
"KMeans Intercluster Distance Map (via MDS)"是一种用于评估KMeans聚类模型性能的工具。
在KMeans聚类中,我们需要选择k值(聚类数),以便将样本划分为k个聚类。一般来说,我们希望每个聚类内部的样本相似度较高,不同聚类之间的样本相似度较低。
KMeans Intercluster Distance Map是一种通过可视化聚类中心之间的距离来帮助我们理解聚类效果的方法。在这种方法中,我们计算每个聚类中心之间的欧几里得距离,并将这些距离绘制成一个热度图。然后,我们使用多维缩放(MDS)算法将这个热度图转换为一个二维或三维的散点图,以便于可视化。
通过观察KMeans Intercluster Distance Map,我们可以得到一些关于聚类的见解。例如,如果聚类中心之间的距离越大,则说明聚类效果越好;如果距离较小,则可能说明聚类效果不太好,或者有些聚类中心之间的样本相似度较高。
值得注意的是,KMeans Intercluster Distance Map只能提供相对的距离度量,不能提供确切的距离值。此外,KMeans Intercluster Distance Map也可能受到随机初始化的影响,不同的运行可能会得到不同的结果。
异常检测
Anomaly_Score:- 在 Isolation Forest 算法中,
Anomaly_Score是基于数据点被隔离所需的路径长度计算的。路径长度越短,数据点越可能是异常值。
- 在 K-Nearest Neighbors (KNN) 算法中,
Anomaly_Score可能是基于数据点到其最近的 k 个邻居的平均距离计算的。距离越大,数据点越可能是异常值。
- 在 Local Outlier Factor (LOF) 算法中,
Anomaly_Score是基于数据点的局部密度与其邻居的局部密度的比值计算的。如果一个数据点的局部密度远低于其邻居,那么它可能是一个异常值。
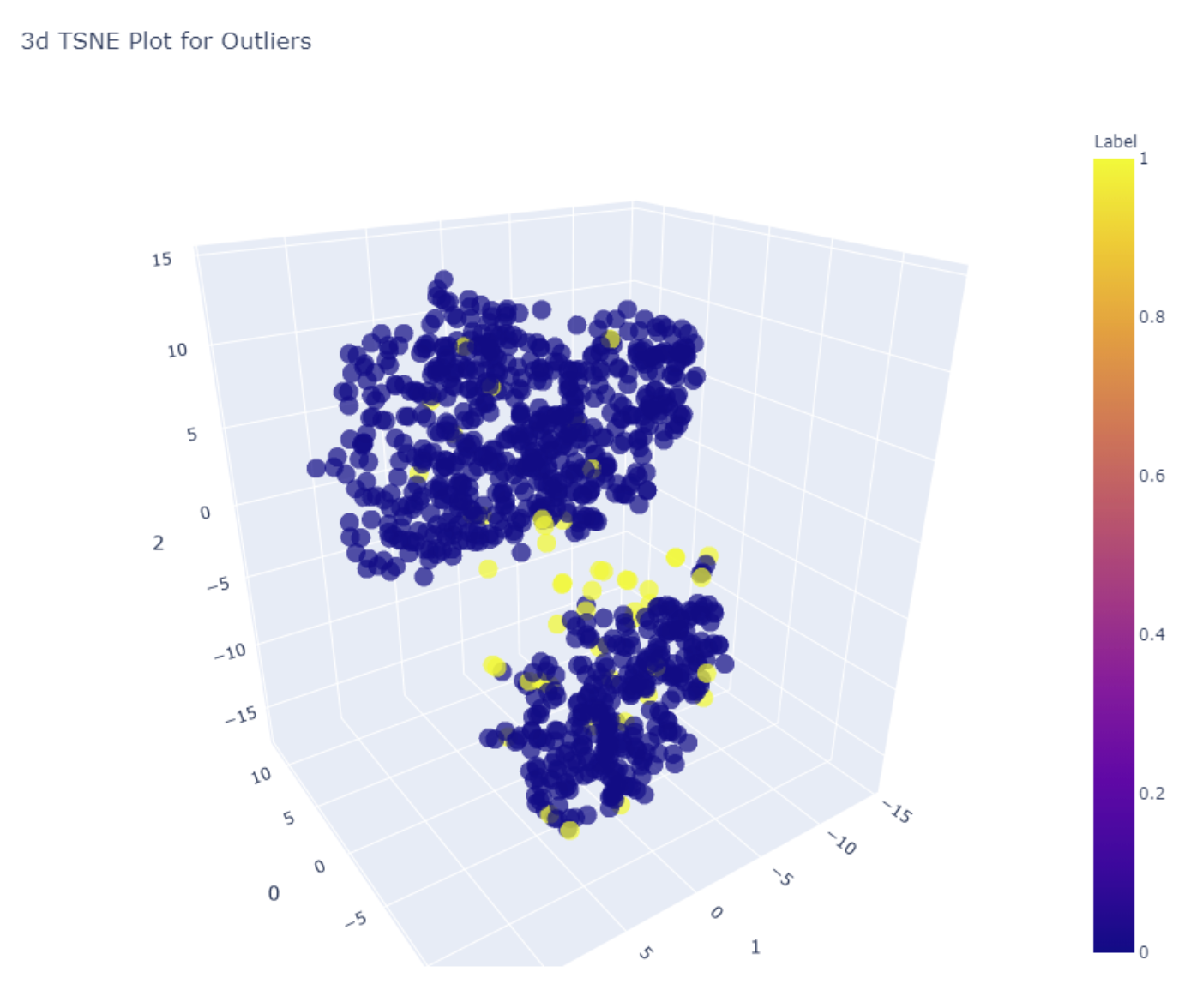
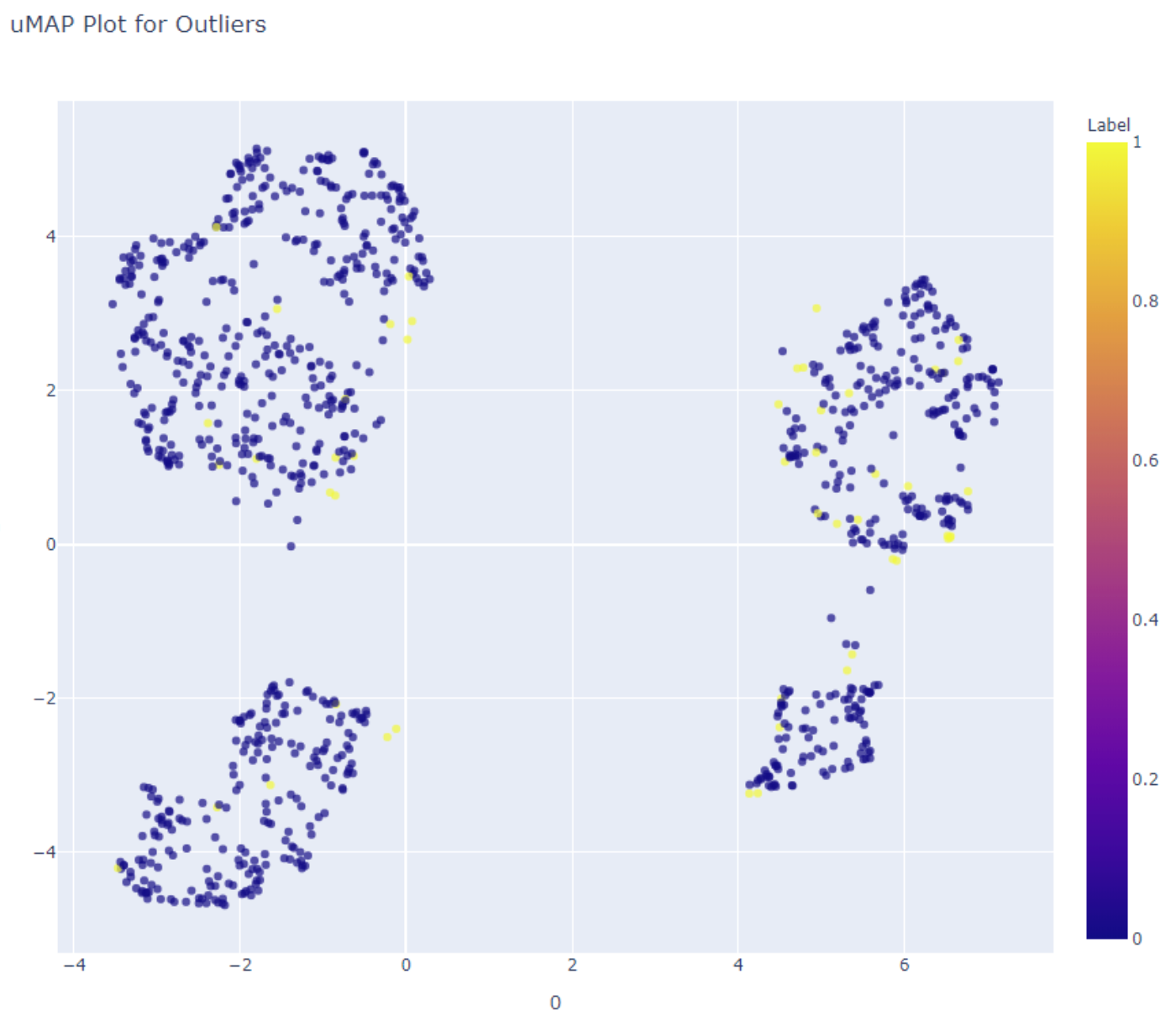
"uMAP Plot for Outliers" 是一种用于异常检测的工具。uMAP(Uniform Manifold Approximation and Projection)是一种降维技术,可以将高维数据投影到低维空间中进行可视化。
在异常检测中,uMAP 可以用于将高维数据投影到二维平面上,以便识别可能存在异常值的任何模式或聚类。uMAP 图可以用于直观地检查数据,并确定与其余数据明显不同的点。
值得注意的是,uMAP 图仅是用于异常检测的工具之一,应与其他方法一起使用以确保准确性。
- 在 Isolation Forest 算法中,
时间序列

- MAE(平均绝对误差):是预测值与真实值之间绝对差值的平均值。它可以衡量模型的预测精度,但不考虑误差的方向。
- RMSE(均方根误差):是预测值与真实值之间差值的平方和与样本数量的比值的平方根。它可以衡量模型的预测精度,并且考虑误差的方向。
- MAPE(平均绝对百分比误差):是预测值与真实值之间绝对百分比误差的平均值。它可以衡量模型的预测精度,但对于小的真实值可能会出现较大的误差。
- SMAPE(对称平均绝对百分比误差):是预测值与真实值之间对称绝对百分比误差的平均值。它可以衡量模型的预测精度,并且对于小的真实值和大的真实值具有相同的权重。
- MASE(平均绝对缩放误差):是预测值与真实值之间绝对误差与历史数据的平均绝对误差的比值。它可以衡量模型的稳健性,因为它不依赖于历史数据的分布情况。
- RMSSE(归一化均方根误差):是预测值与真实值之间差值的平方和与历史数据的平方平均值的比值的平方根。它可以衡量模型的预测精度,并且考虑历史数据的分布情况。
- R2(决定系数):是预测值与真实值之间相关性的平方。它可以衡量模型的预测精度,但对于具有不同数据范围的变量可能会失效。
这些指标的选择取决于问题的性质和具体的应用场景。
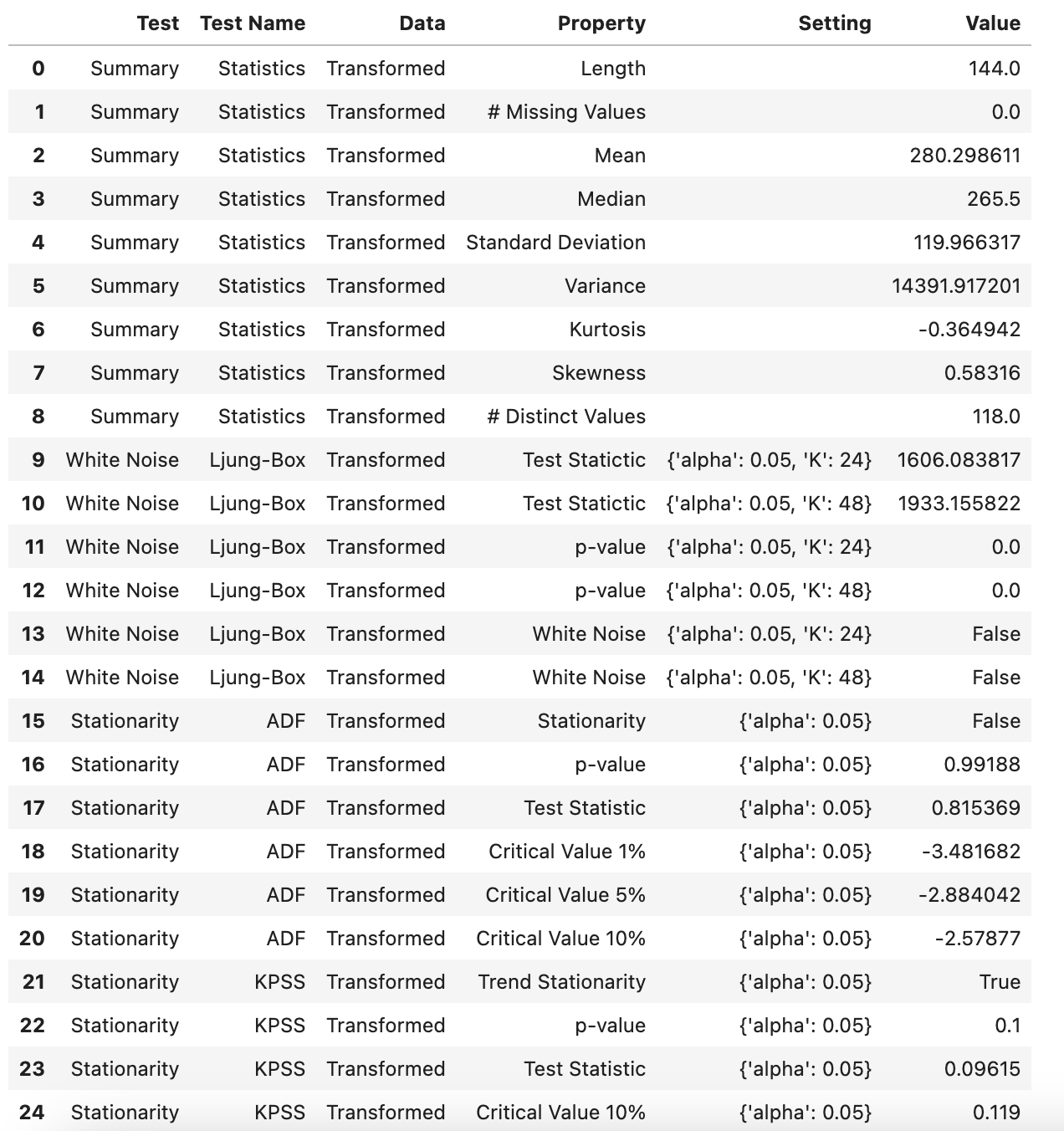
这是一份详细的统计测试报告,其中包含了对时间序列数据进行的各种统计检验的结果。以下是对这些结果的解释:
- Summary Statistics: 这部分提供了数据的一些基本统计信息,包括数据的长度、缺失值的数量、均值、中位数、标准差、方差、峰度、偏度以及不同值的数量。
- White Noise Ljung-Box: 这部分的结果是 Ljung-Box 测试的结果,这是一个用于检验数据是否是白噪声的统计测试。如果 p 值小于显著性水平(这里是 0.05),那么我们可以拒绝原假设(数据是白噪声)。在这个例子中,p 值为 0,所以我们可以拒绝原假设,即数据不是白噪声。
- Stationarity ADF: 这部分的结果是 Augmented Dickey-Fuller (ADF) 测试的结果,这是一个用于检验数据是否是平稳的统计测试。如果 p 值小于显著性水平,那么我们可以拒绝原假设(数据是非平稳的)。在这个例子中,p 值为 0.99188,所以我们不能拒绝原假设,即数据是非平稳的。
- Stationarity KPSS: 这部分的结果是 Kwiatkowski-Phillips-Schmidt-Shin (KPSS) 测试的结果,这也是一个用于检验数据是否是平稳的统计测试,但是它的原假设和 ADF 测试相反。如果 p 值大于显著性水平,那么我们不能拒绝原假设(数据是平稳的)。在这个例子中,p 值为 0.1,所以我们不能拒绝原假设,即数据是平稳的。
- Normality Shapiro: 这部分的结果是 Shapiro-Wilk 测试的结果,这是一个用于检验数据是否符合正态分布的统计测试。如果 p 值小于显著性水平,那么我们可以拒绝原假设(数据符合正态分布)。在这个例子中,p 值为 0.000068,所以我们可以拒绝原假设,即数据不符合正态分布。
这些统计检验的结果可以帮助我们更好地理解数据的特性,以及选择合适的模型。
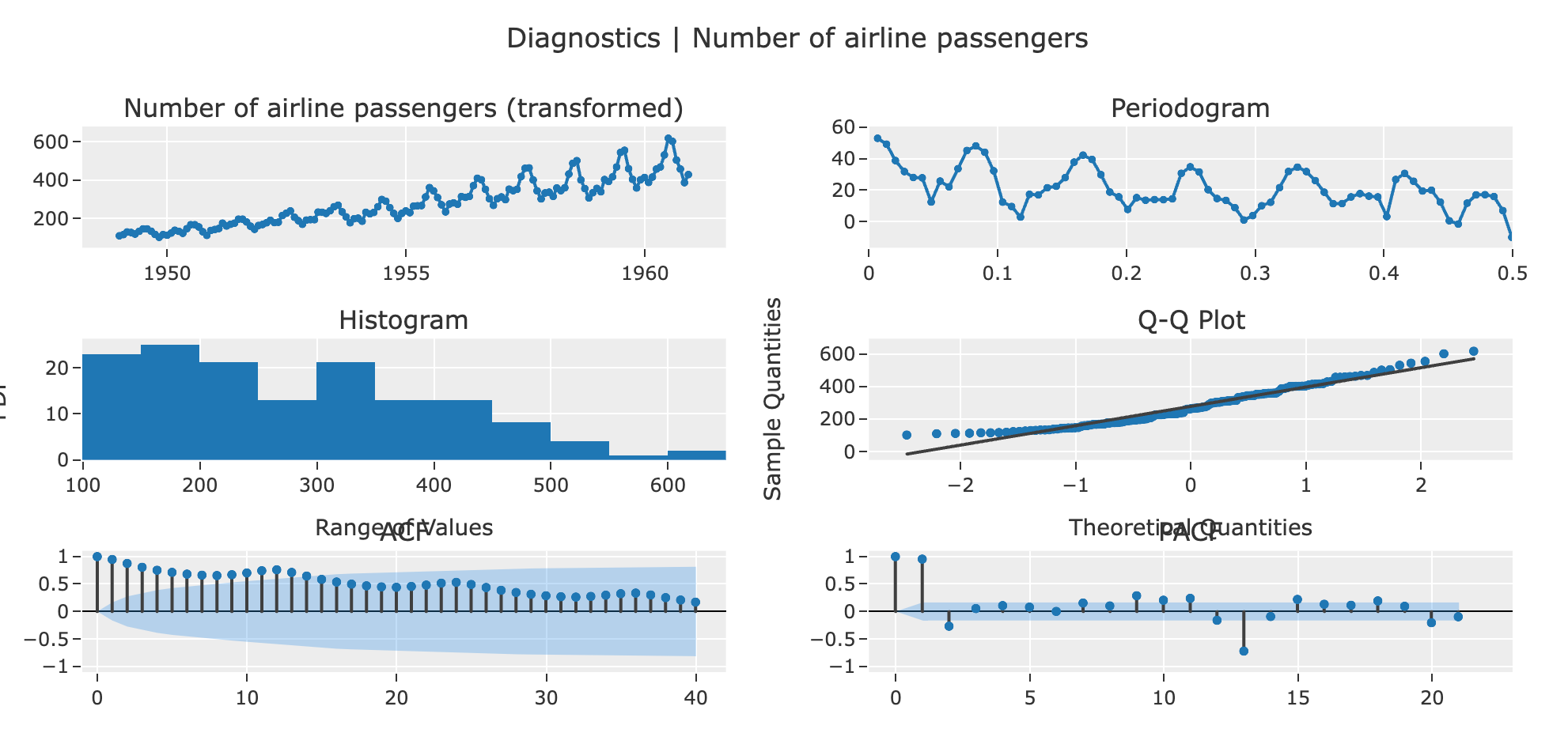
自定义评估指标
在机器学习中,Custom Metric(自定义度量)是一种评价模型性能的重要工具,它可以帮助我们更深入地理解模型的性能和其在特定上下文中的表现。以下是一些可能需要自定义度量的情况:
- 特定业务需求:标准的度量标准可能无法充分反映你的特定业务需求或目标。例如,你可能更关心模型在某个特定类别上的性能,或者更关心模型在某种特定情况下的误报和漏报。在这些情况下,你可能需要创建自定义的度量标准,以便更准确地衡量你关心的性能。
- 不平衡数据集:对于不平衡的数据集,常规的评估指标(如准确度)可能无法提供有用的信息,因为它们可能会被主导类别所主导。在这种情况下,可以使用自定义度量(例如,精确度,召回率,F1分数等)来更好地评估模型在较小类别上的性能。
- 特殊评价指标:在某些竞赛或项目中,可能会有特殊的评价指标,这需要你创建一个与该指标对应的自定义度量。
- 优化模型:有时,你可能希望模型优化特定的度量标准,而不是默认的度量标准。在这种情况下,你可以创建一个自定义度量,并在模型训练时使用它作为优化目标。
总的来说,自定义度量可以为模型提供更精细的优化和评估方式,使得模型能更好地满足实际应用的需求。
假设你正在为一个电信公司开发一个机器学习模型,用于预测哪些客户最可能在合同到期后不再续约,也就是所谓的客户流失。该模型的目标是允许公司更有效地使用其营销资源,通过识别并主动接触那些最有可能离开的客户,然后向他们提供激励来留住他们。
在这种情况下,我们可以做以下商业价值假设:
- 每个客户每年为公司带来的收入为$500
- 通过提供折扣或其他激励措施,留住一个客户的成本为$100
- 如果模型错误地将一个客户标记为可能离开,而实际上他们不会离开,公司可能会不必要地花费$100来提供激励
- 如果模型错过了一个实际会离开的客户(即误报),那么公司将失去的收入为$500
使用这些假设,我们可以为模型的预测结果分配具体的经济价值。例如,如果模型准确地预测了1000个会离开的客户,并且所有这些客户在被提供激励后都选择留下,那么模型将为公司节省$400,000(即500,000 - 100,000)的潜在损失。然而,如果模型错误地预测了500个不会离开的客户,那么这将产生$50,000的额外成本。
这个例子展示了如何在具体的商业背景中为机器学习模型赋予经济价值。然而,要记住的一点是,为了实现这个目标,模型需要针对与业务相关的指标进行训练和优化,而不仅仅是传统的机器学习性能指标。
假设商业银行想要预测可能申请小型企业贷款的潜在客户。目标是通过模型识别最有可能申请小型企业贷款的潜在客户。
为了理解这个贷款预测模型的商业价值,我们可以做一些假设:
- 贷款成功的每个客户将为银行带来3000美元的利润。
- 花费在营销和行政工作上以吸引和处理每个潜在贷款客户的成本是200美元。
- 被模型错误标记为可能申请贷款的客户(假阳性)将使银行产生200美元的无效营销成本。
- 被模型漏掉的贷款客户(假阴性)会导致银行损失3000美元的潜在利润。
如果我们将这些具有商业特性的成本和利润应用于我们模型的表现,我们可以计算出其商业价值。例如,如果我们的模型正确地识别了1000个可能申请贷款的客户(真阳性),错误地识别了300个(假阳性),同时错过了150个后来确实申请贷款的客户(假阴性),利润可以按照以下方式计算:
利润 = (1000 * $3000) - (1000 * $200) - (300 * $200) - (150 * $3000) = $2,140,000
尽管模型在准确性、精确性或召回率方面可能并不是最佳的,但在这个特定的上下文中,它为公司带来了显著的商业价值,通过最大化利润。然而,重要的是要理解模型应作为决策工具的一部分使用,并且需要持续监控其性能,并根据业务环境的变化进行调整。
模型解释
SHAP (SHapley Additive exPlanations) 是一种用于解释机器学习模型预测结果的方法。SHAP 值可以帮助我们理解每个特征对模型预测的贡献。
让我们通过一个简单的例子来解释 SHAP。
假设我们有一个预测房价的模型,输入特征包括房屋的面积(Area)、卧室数量(Bedrooms)和地理位置(Location)。对于一个具体的房屋,模型预测其价格为 300,000 美元,而整个训练数据集的平均房价为 200,000 美元。
我们可以计算每个特征的 SHAP 值,以理解它们各自对预测价格的贡献。例如,我们可能发现:
- Area 的 SHAP 值为 +50,000 美元。这意味着,相比于平均房屋,这个房屋由于面积大,价格增加了 50,000 美元。
- Bedrooms 的 SHAP 值为 +20,000 美元。这意味着,由于这个房屋的卧室数量,价格增加了 20,000 美元。
- Location 的 SHAP 值为 +30,000 美元。这意味着,由于这个房屋的地理位置,价格增加了 30,000 美元。
这些 SHAP 值的总和(+50,000 +20,000 +30,000 = +100,000 美元)正好等于这个房屋的预测价格(300,000 美元)减去平均房价(200,000 美元)。这就是 SHAP 的加性特性。
通过 SHAP 值,我们可以清楚地看到每个特征对预测结果的贡献,从而理解模型的预测行为。
SHAP值有以下几个重要的性质:
- 加性:所有特征的SHAP值之和等于预测值减去基线值(通常是训练数据的平均预测值)。
- 对称:如果两个特征对模型的贡献相同,那么它们的SHAP值应该相同。
- 零和:如果一个特征没有对模型的预测做出任何贡献,那么它的SHAP值应该为零。
通过计算和分析SHAP值,我们可以理解每个特征对模型预测的影响,从而提高模型的可解释性。
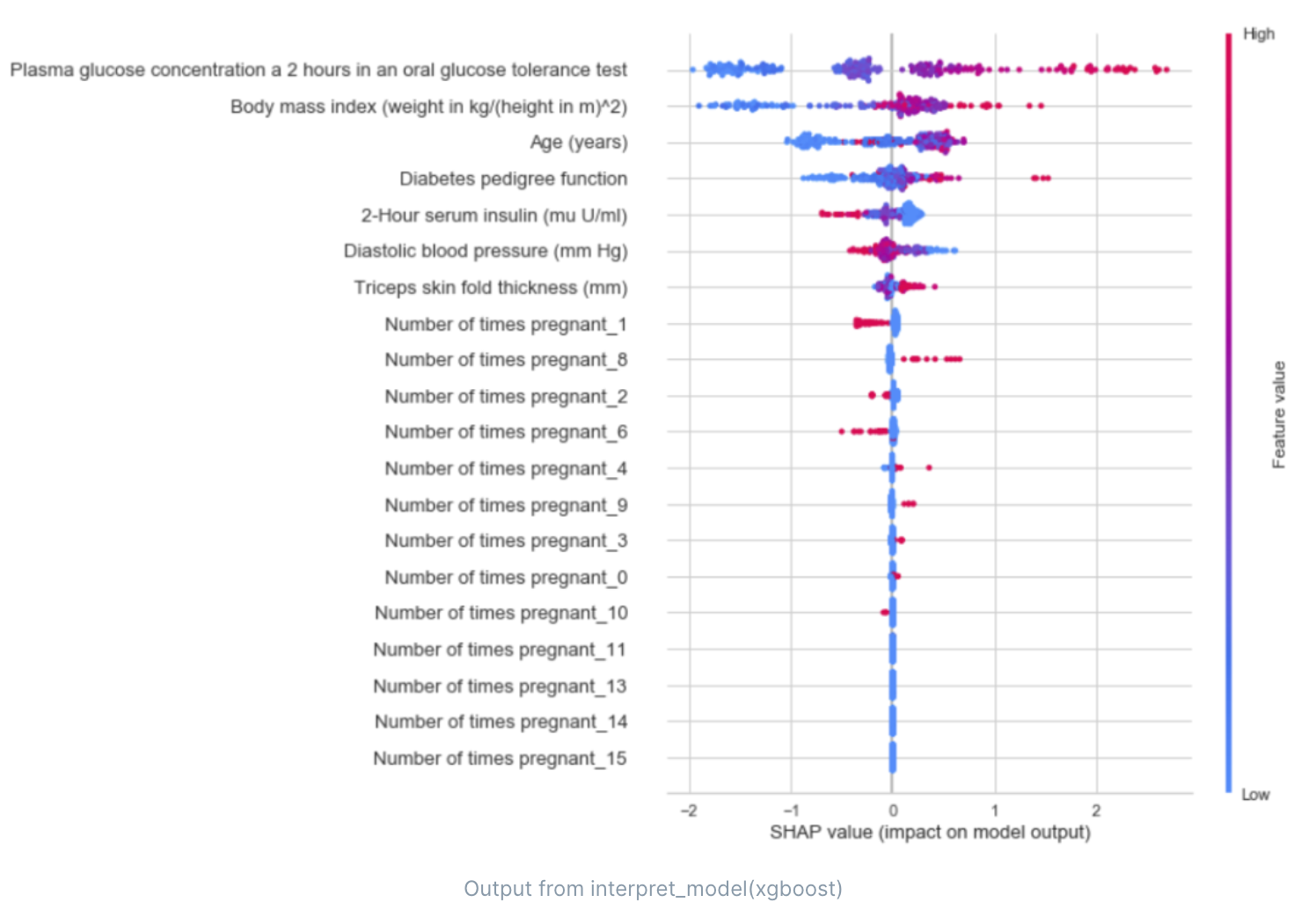
这个图是一个SHAP值图,它是一种用于解释模型预测的强大工具。SHAP值可以帮助我们理解每个特征对模型预测的贡献,以及这些特征的影响是正面的还是负面的。
在图中,每个点代表一个观察值。横坐标表示SHAP值,也就是该特征对预测结果的贡献。纵坐标是特征名称,颜色表示特征值的大小(红色表示高,蓝色表示低)。
- 特征的重要性:特征在图中的位置(从上到下)是根据其对输出的影响程度排序的。最上面的特征对模型的预测影响最大。
- 特征的影响方向:如果一个特征的大部分点在图的右侧,那么这个特征的较大值会导致模型的预测结果增加;如果一个特征的大部分点在图的左侧,那么这个特征的较大值会导致模型的预测结果减少。
- 特征的影响大小:点的横坐标表示该特征对预测结果的影响大小。点越远离中心线,表示该特征对预测结果的影响越大。
通过这个图,我们可以更好地理解模型的预测行为,以及哪些特征对预测结果的影响最大。
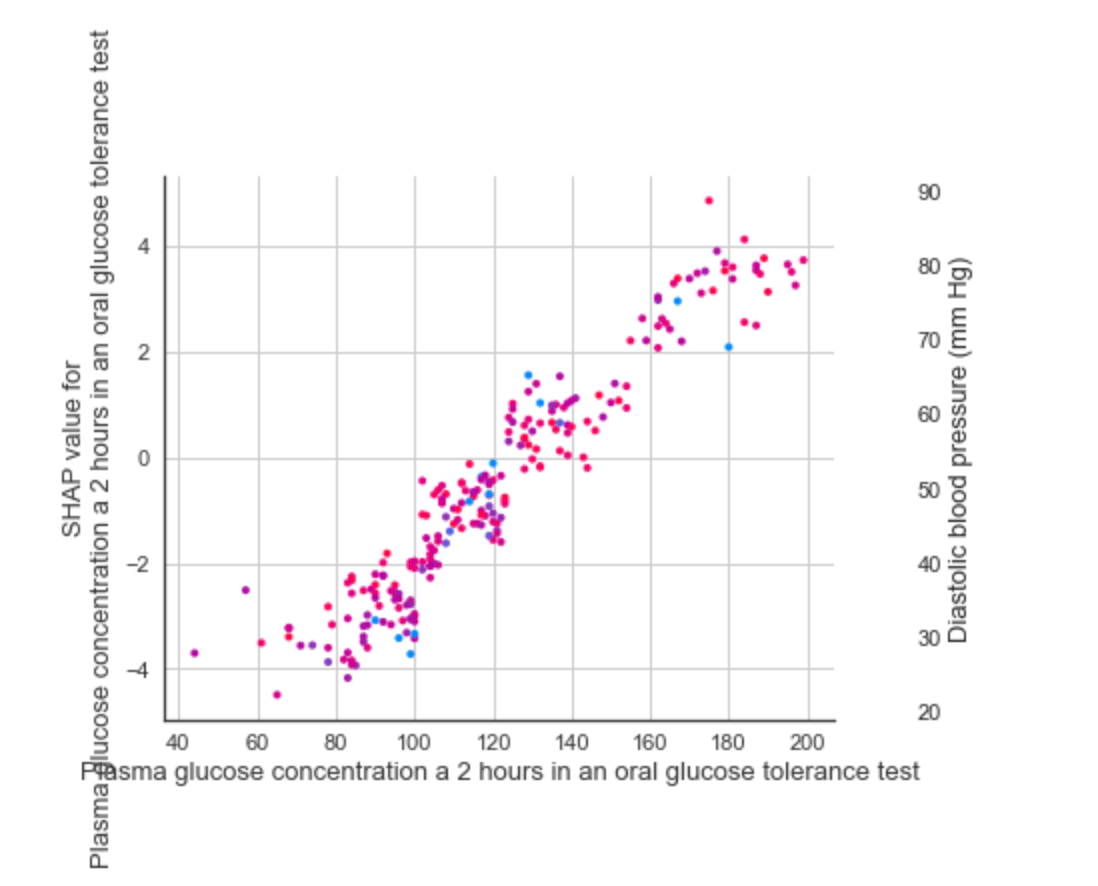
这个图是一个特征相关性图,它展示了特征之间的相关性以及特征对模型预测的影响。
在这个图中,每个点代表一个观察值。横坐标是一个特征的SHAP值,纵坐标是另一个特征的SHAP值。颜色表示模型预测的结果。
这个图可以帮助我们理解以下几点:
- 特征之间的相关性:如果两个特征的点在图中形成一条明显的直线(无论是正斜率还是负斜率),那么这两个特征可能存在强相关性。
- 特征对模型预测的影响:颜色表示模型预测的结果。例如,红色可能表示模型预测的结果为1,蓝色可能表示模型预测的结果为0。通过颜色,我们可以看出特征的SHAP值如何影响模型的预测。
通过这个图,我们可以更好地理解特征之间的关系以及它们如何影响模型的预测。
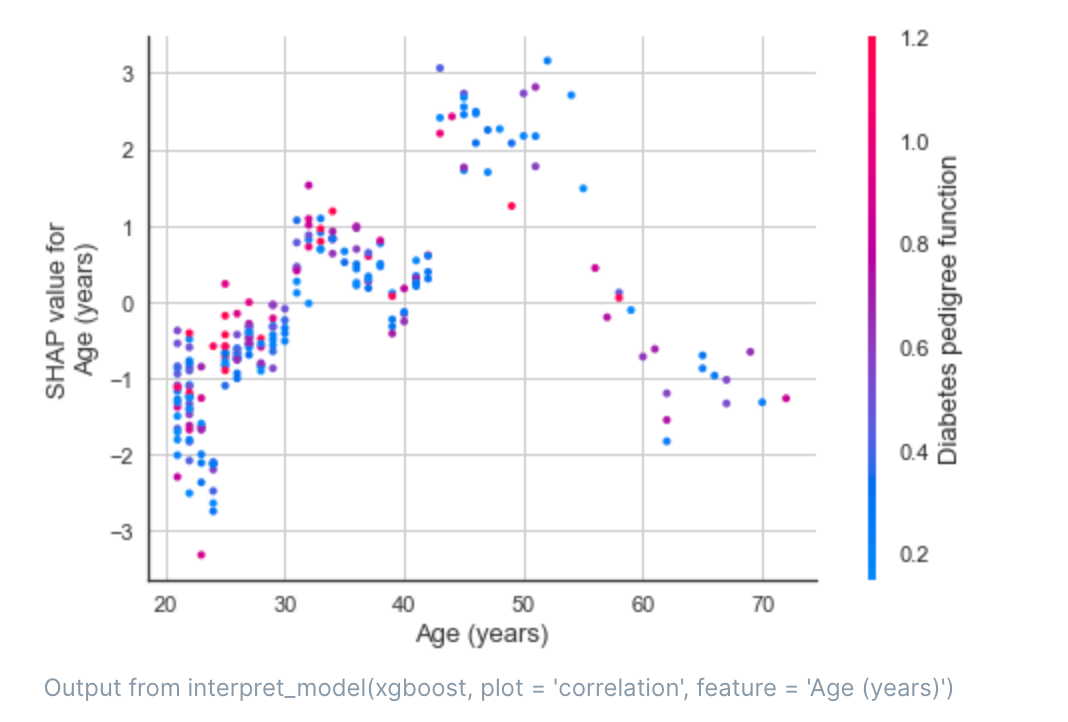
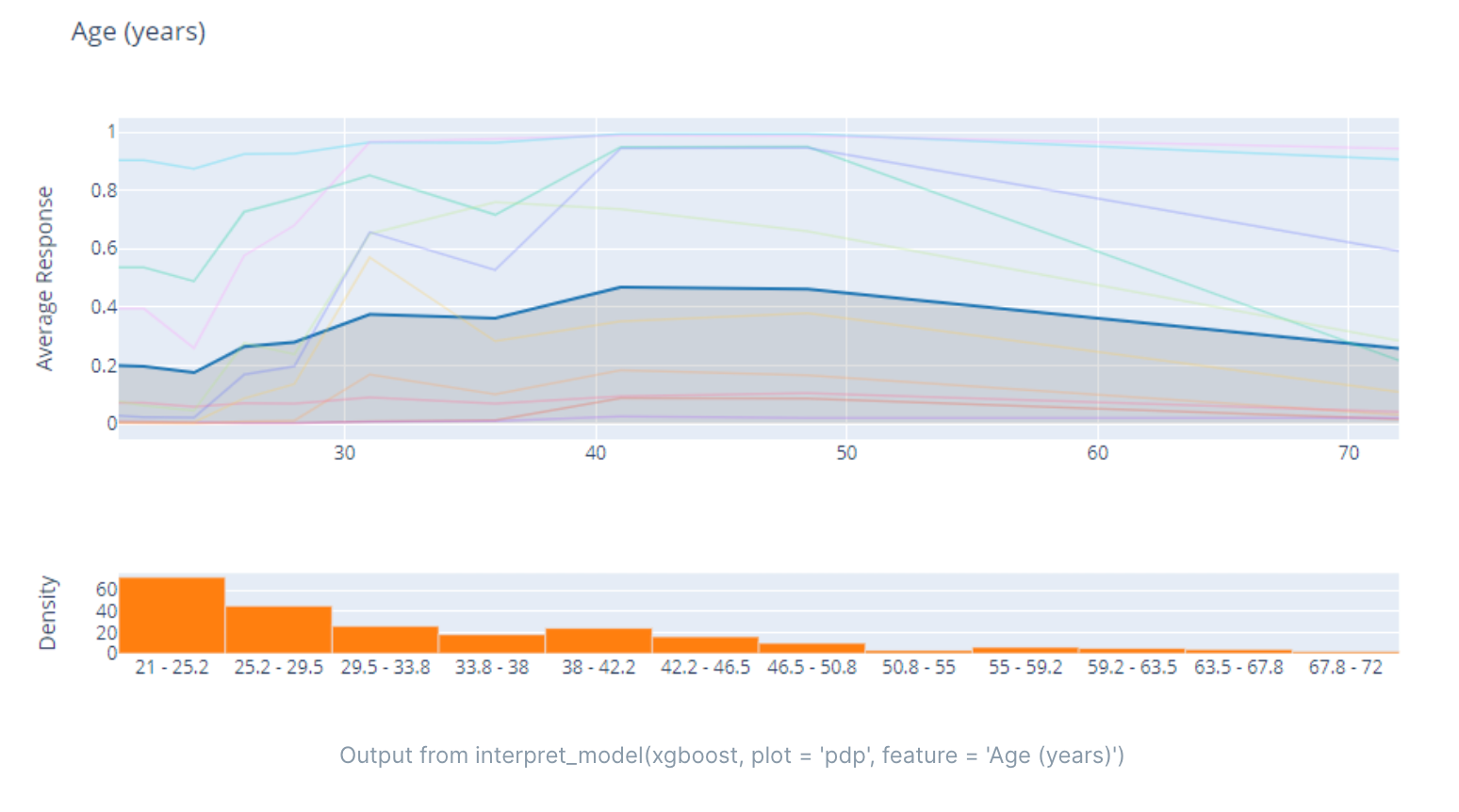
如图:年龄在20-40之间,糖尿病谱系功能指数越高,年龄的贡献度越大,40岁以上,从这2个特征来的,贡献度主要受年龄影响,和糖尿病谱系功能指数关系不大。
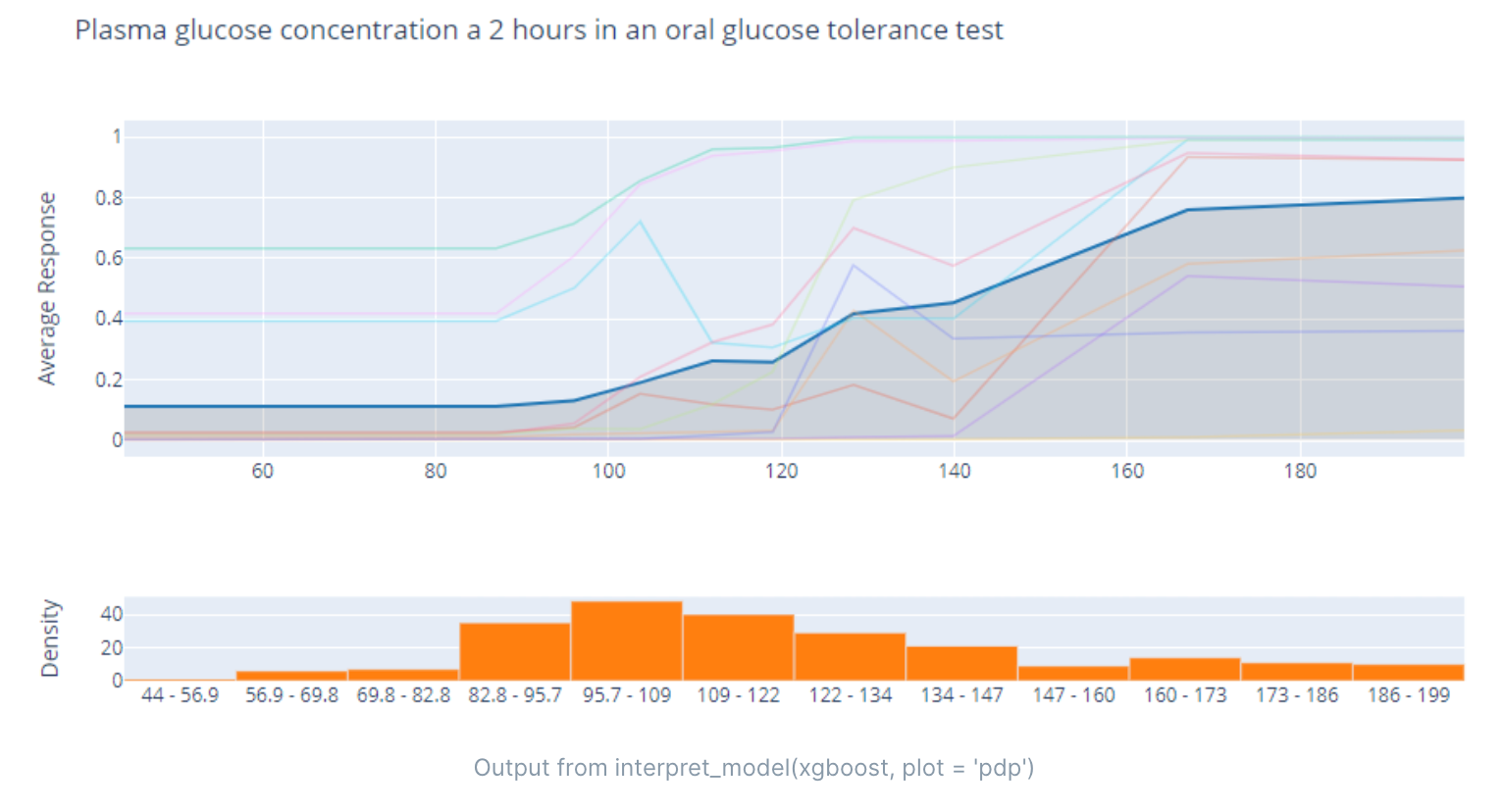
Plasma glucose concentration a 2 hours in an oral glucose tolerance test(餐后2小时血浆葡萄糖浓度)是一种测量人体对葡萄糖的代谢能力的方法。这个测试通常用于诊断糖尿病或糖尿病前期。在这个测试中,患者需要饮用含有75克葡萄糖的饮料,并在饮用后2小时测量血浆葡萄糖浓度。根据这个结果,医生可以确定患者的血糖控制情况,并诊断是否存在糖尿病或糖尿病前期。正常的餐后2小时血浆葡萄糖浓度应该低于140毫克/分升。
PDP(Partial Dependence Plot,偏依赖性图)是一种用于可视化特征和目标变量之间关系的方法。PDP 可以帮助我们理解特征和目标变量之间的非线性关系,以及每个特征对目标变量的影响程度。
PDP 的基本思想是将某个特征固定在特定的取值上,然后观察目标变量的变化情况。在这个过程中,其他特征的取值保持不变。通过对多个特定取值进行观察,我们可以得到特征与目标变量之间的关系。
例如,我们可以使用 PDP 来理解一个房价预测模型中面积和房价之间的关系。我们可以选择一些面积的取值(如 50 平方米、100 平方米、150 平方米),然后分别观察这些取值下房价的变化情况。通过这些观察结果,我们可以得到面积与房价之间的非线性关系,以及每个面积取值对房价的影响程度。
PDP 可以用于任何类型的机器学习模型,包括线性模型和非线性模型。它可以帮助我们理解特征与目标变量之间的关系,从而提高模型的可解释性。
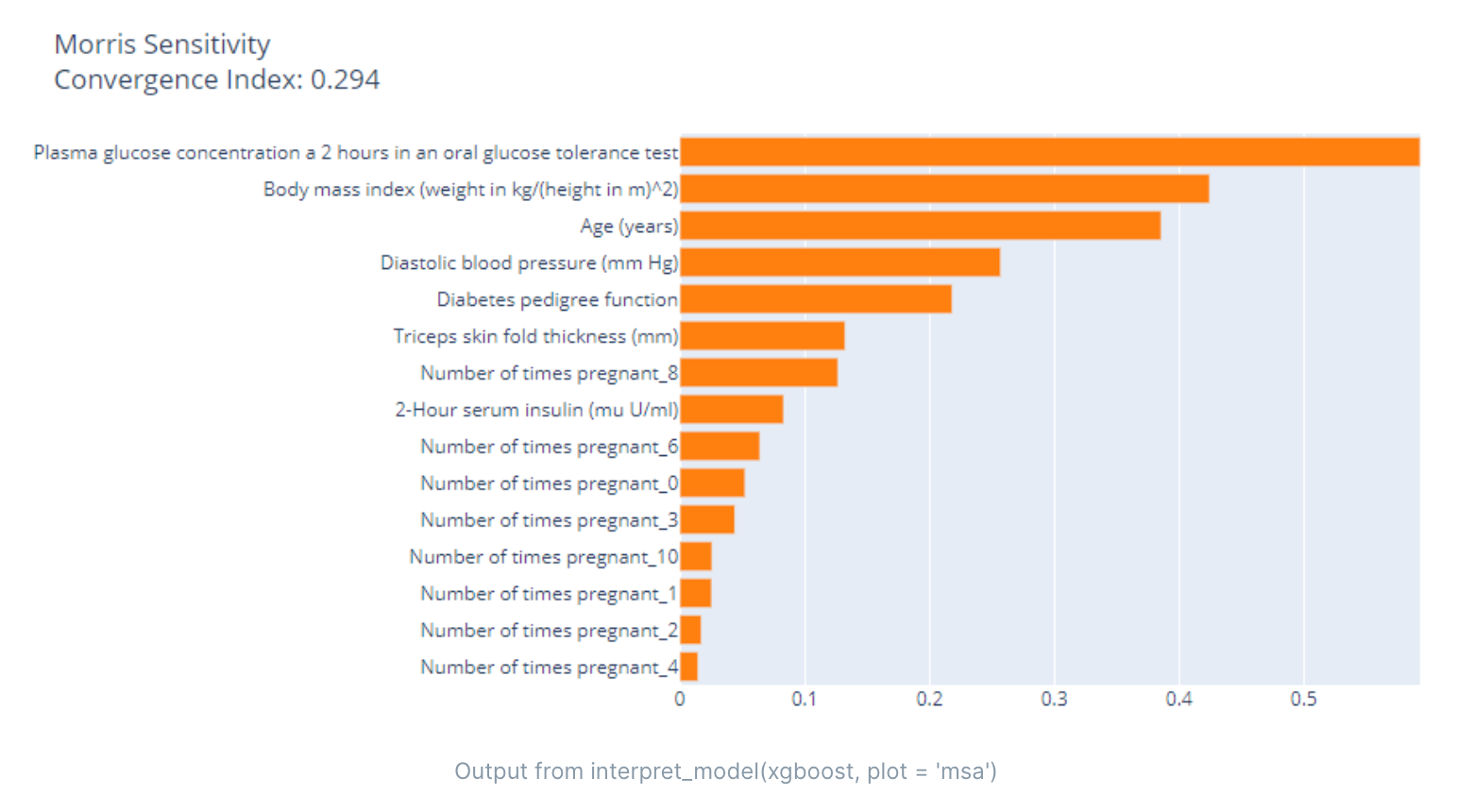
Morris敏感度分析是一种用于评估模型输入变量对输出变量的影响的方法。该方法通过在输入变量上进行随机扰动,然后测量对输出变量的影响程度,以确定哪些变量对输出变量有较大的影响。
Morris敏感度分析可以用于任何类型的模型,包括线性模型、非线性模型和机器学习模型。它可以帮助我们理解模型输入变量之间的相互作用关系,以及确定哪些变量对模型输出的影响最大。
Morris敏感度分析的基本步骤如下:
- 确定要分析的输入变量和输出变量。
- 对每个输入变量,生成一组随机样本,并将其添加到原始输入变量值中,形成新的输入变量值。这个过程称为扰动(perturbation)。
- 使用扰动后的输入变量值重新运行模型,并记录输出变量的值。
- 重复步骤2和步骤3,生成多组扰动样本,并记录每个输入变量的平均影响程度。
- 根据每个输入变量的平均影响程度,进行敏感度排序,以确定哪些变量对输出变量的影响最大。
Morris敏感度分析是一种简单而有效的方法,它可以帮助我们理解模型输入变量之间的相互作用关系,以及确定哪些变量对模型输出的影响最大。它可以用于各种类型的模型,包括线性模型、非线性模型和机器学习模型。
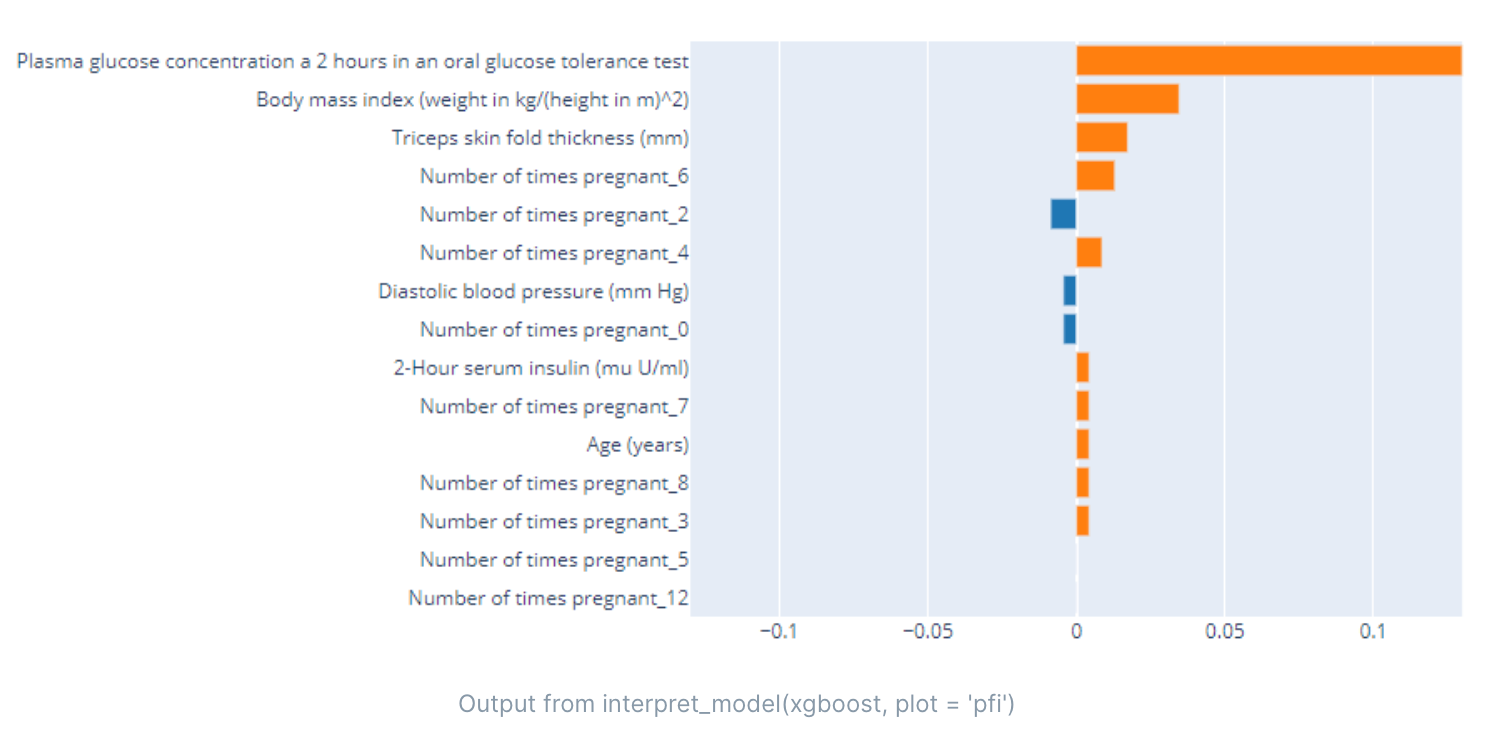
PFI(Permutation Feature Importance,排列特征重要性)是一种用于评估机器学习模型中特征重要性的方法。该方法通过随机打乱某个特征的值,然后测量对模型性能的影响程度,以确定哪些特征对模型性能的影响最大。
PFI 可以用于任何类型的机器学习模型,包括线性模型、非线性模型和深度学习模型。它可以帮助我们理解模型中各个特征的重要性,从而提高模型的可解释性。
PFI 的基本步骤如下:
- 确定要分析的特征和模型性能指标(如准确率、AUC)。
- 对每个特征,将其值打乱,并使用打乱后的数据集重新训练模型,并记录模型性能指标的值。
- 重复步骤2多次,生成多组打乱样本,并记录每个特征的平均影响程度。
- 根据每个特征的平均影响程度,进行特征排序,以确定哪些特征对模型性能的影响最大。
PFI 是一种简单而有效的方法,它可以帮助我们理解模型中各个特征的重要性,从而提高模型的可解释性。它可以用于任何类型的机器学习模型,并且可以与其他解释性方法(如 SHAP 值、PDP)结合使用,以提高模型的解释性能。
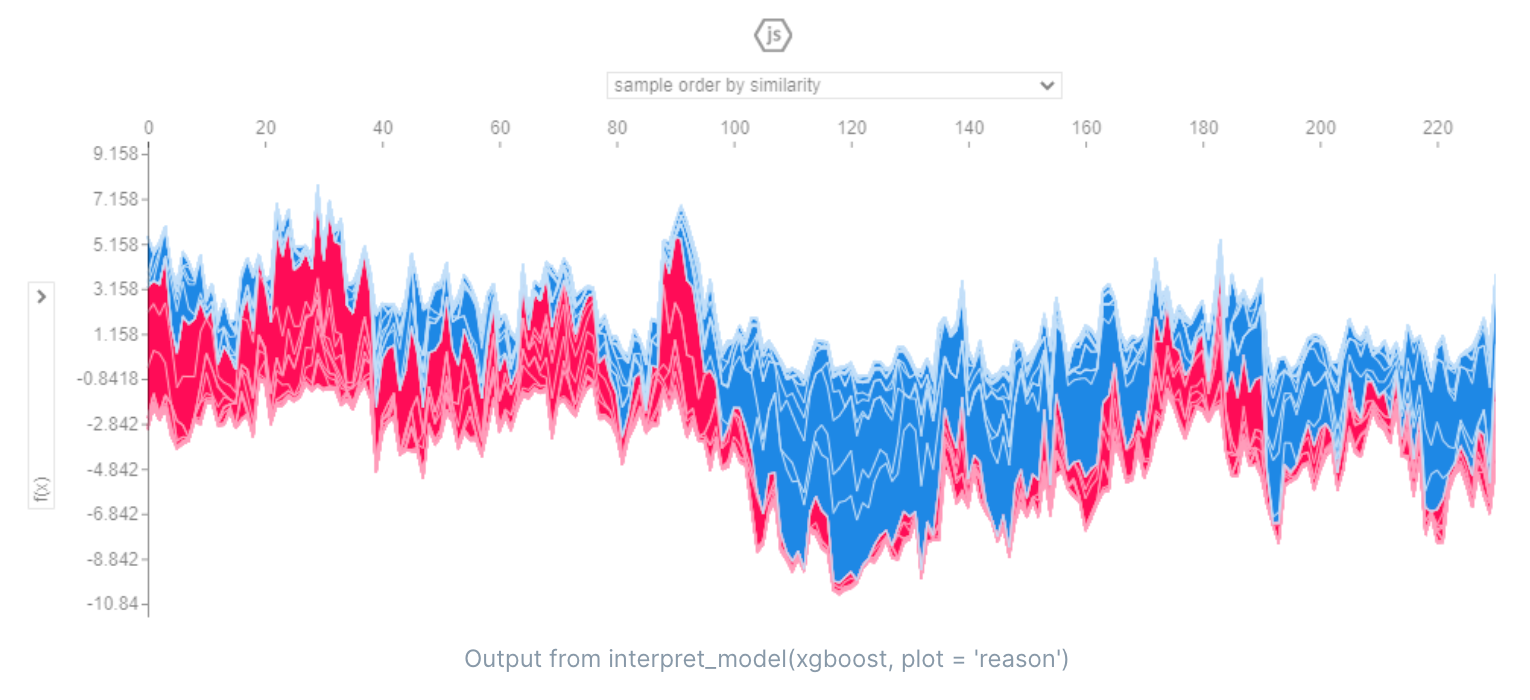
SHAP(SHapley Additive exPlanations)是一种用于解释机器学习模型输出的方法。它基于 Shapley value 的概念,通过计算每个特征对预测结果的贡献,帮助我们理解模型的预测行为。
SHAP 的核心思想是,将每个特征的取值看作一个“贡献者”,然后计算每个“贡献者”的贡献值。这个方法类似于博弈论中的 Shapley value,它可以帮助我们理解每个“贡献者”对最终预测结果的贡献程度。
SHAP 的核心算法是一种基于树模型的算法,它可以计算每个特征对预测结果的贡献值。SHAP 的结果是一个“reason plot”,它可以帮助我们理解每个特征对预测结果的影响,以及特征之间的相互作用关系。
在机器学习中,SHAP 的 reason plot 可以帮助我们理解每个特征对模型输出的贡献,以及特征之间的相互作用关系。它可以帮助我们识别哪些特征对模型输出最为重要,进而优化模型的预测性能。
具体来说,reason plot 可以帮助我们回答以下问题:
- 每个特征对模型输出的贡献是多少?
- 特征之间存在什么样的相互作用关系?
- 特征的取值范围对预测结果有什么影响?
- 模型的预测输出是否合理?
通过分析 SHAP 的 reason plot,我们可以深入了解模型如何做出预测,从而提高模型的可解释性和预测性能。

SHAP(SHapley Additive exPlanations)是一种解释性机器学习方法,可以帮助我们理解模型输出的贡献度。SHAP 的核心思想是将每个特征的取值看作一个“贡献者”,并计算每个“贡献者”的贡献值。该方法类似于博弈论中的 Shapley value,它可以帮助我们理解每个“贡献者”对最终预测结果的贡献程度。
SHAP 的 force plot 是一种用于可视化 SHAP 值的方法,它可以帮助我们理解每个特征对预测结果的贡献,以及特征之间的相互作用关系。force plot 的基本思想是,将每个样本的 SHAP 值拆分成每个特征的 SHAP 值,并将它们可视化成一个条形图。通过这个条形图,我们可以直观地看到每个特征对预测结果的贡献程度,以及特征之间的相互作用关系。
具体来说,force plot 可以帮助我们回答以下问题:
- 每个特征对预测结果的贡献是多少?
- 特征之间存在什么样的相互作用关系?
- 每个样本对预测结果的贡献是多少?
- 预测结果是否合理?
通过分析 force plot,我们可以深入了解模型如何做出预测,从而提高模型的可解释性和预测性能。
具体来说,我们可以使用 force plot 来回答以下问题:
- 对于某个特定样本,每个特征对预测结果的贡献是多少?
- 特征之间存在什么样的相互作用关系?
- 预测结果是否合理?
通过对 force plot 的分析,我们可以更好地理解模型如何做出预测,从而优化模型的预测性能。